Substitua o sistema de forças e de momentos binários por uma força resultante e um momento equivalente ao sistema no ponto . Expresse os resultados na forma de vetores cartesianos.
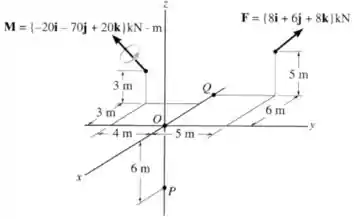
Passo 1
Como temos uma única força atuando no sistema, a nossa substituição vai apenas trocar o ponto de aplicação da força , então continuamos com:
Mas quando nós deslocarmos essa força para o ponto, o momento produzido por ela vai mudar, e precisamos compensar isso com um novo momento.
Passo 2
Vamos calcular o momento resultante do sistema original em relação ao ponto . Fazemos isso porque quando a força estiver em , o momento gerado por ela será nulo em relação a esse ponto.
Então, para manter o mesmo efeito final no sistema, temos que aplicar um momento igual ao que existia antes;
O primeiro termo do lado direito é simplesmente o vetor de momento que foi dado no desenho:
E o segundo termo é o produto vetorial de (que é o vetor positção que liga o ponto ao ponto de aplicação da força ) e a própria força. Vamos começar escrevendo esse vetor :
Então:
Agora é só substituir tudo na primeira fórmula:
Pronto, esse é o momento que precisamos aplicar para “repôr” o que foi perdido com o deslocamento da força e com a eliminação do momento .
Resposta
O sistema pode ser substituído pela força aplicada no ponto e pelo momento .