Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 4.9 - Ex. 113
Substitua as três forças atuantes no cano por uma única força resultante. Especifique onde a força atua, tomando a extremidade como referência.
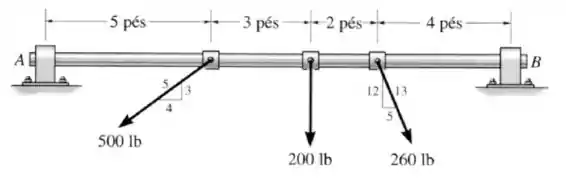
Passo 1
Vamos começar escrevendo cada uma das forças do desenho em forma vetorial:
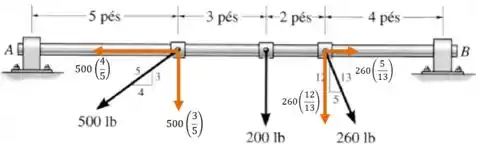
Começando da esquerda para a direita:
E então a força resultante será:
Passo 2
E podemos definir esse vetor usando sua intensidade e um ângulo:
E como as duas componentes do vetor são negativas, vamos tomar como referência o ângulo que ele forma com o semieixo horizontal negativo:
Passo 3
Agora vamos calcular o momento resultante do sistema de três forças em relação ao ponto .
Todas as componentes horizontais das forças terão momento nulo em relaçao a , já que a distância perpendicular dessas componentes até o ponto é zero.
Então ficamos apenas com o seguinte:
E todas aparecem com sinal positivo porque todas favorecem a rotação no sentido anti-horário em torno de .
Passo 4
Se nós queremos substituir essas três forças por uma única força a uma distância do ponto , ela terá que produzir esse mesmo momento !
Mas o momento da força (assim como das anteriores) só vai depender da sua componente vertical e da sua distância até o ponto , ou seja:
Resposta
O sistema pode ser substituído por uma única força a do semieixo horizontal negativo, localizada a pés do ponto , ao longo da barra .