Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 4.10 - Ex. 157
Substitua o carregamento por uma força e um momento equivalentes atuantes no ponto .
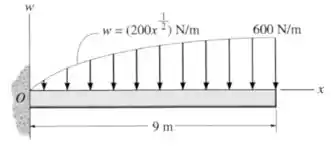
Passo 1
O primeiro passo aqui é calcular a força total produzida pela distribuição de forças. Para fazer isso, temos que calcular a área da distribuição.
A melhor forma de calcular essa área é utilizar uma integral:
Então aquela distribuição é equivalente a uma força de de intensidade, apontando na vertical para baixo.
Passo 2
Para calcular o momento gerado por essa distrubição (em relação ao ponto ), podemos usar outra integral:
Onde o sinal negativo aparece porque as forças favorecem a rotação no sentido horário, e estamos multiplicando a função da distribuição por , que é a distância perpendicular de cada ponto até .
Ou seja, temos que aplicar um momento de no sentido horário.
Resposta
O carregamento pode ser substituído por uma força de apontando na vertical para baixo, sobre o ponto , e um momento de no sentido horário.