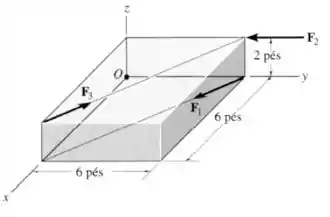
As três forças que atuam no bloco têm, cada uma intensidade de . Substitua esse sistema por um torsor e especifique o ponto em que sua linha de ação intercepa o eixo , tomando como referência o ponto .
Passo 1
Vamos começar calculando a força resultante que age sobre o bloco, sabendo que todas elas têm o mesmo módulo:
As forças e tem a mesma direção, mas sentidos opostos, então logo de início já sabemos que vão se cancelar. Por isso ficamos apenas com a força para a nossa resultante:
Passo 2
E vamos calcular também o momento total dessas forças em relação ao ponto .
O par , forma um binário, já que são duas forças de mesmo módulo e direção, sentidos opostos e separadas por uma distância perpendicular de .
Pelo desenho, vemos que as forças estão sobre a diagonal de um quadrado de lado , então o ângulo entre essas forças e os eixos é :
E para calcular o momento da força precisamos usar um produto vetorial:
Agora é só somar tudo:
Passo 3
Para substituir esse sistema por um torsor, teríamos que utilizar um momento alinhado à nossa força resultante :
Essa força, por ser paralela ao eixo , não produz nenhum momento em . Mas nós vimos que o nosso sistema inicial tinha uma componente de momento em :
Então o momento do nosso torsor deve ser:
E resta para a nossa força produzir a outra componente do momento resultante que nós calculamos:
Para que essa força produza apenas momento em , ela precisa estar no plano , e podemos calcular sua coordenada da seguinte forma:
Pronto, já temos tudo o que é necessário para definir um torsor.
Resposta
O sistema pode ser substituído por um torsor com e , agindo em uma altura no plano .