Substitua o sistema de forças atuantes sobre a estrutura por uma força resultante e um momento equivalentes ao sistema sobre o ponto .
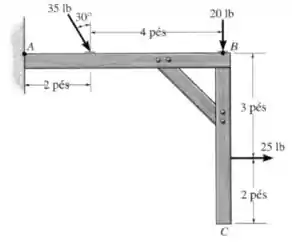
Passo 1
Vamos começar escrevendo cada uma das forças do desenho em forma vetorial, começando da esquerda para a direita:
E então a força resultante é:
Passo 2
Podemos descrever esse vetor completamente usando uma intensidade e um ângulo:
E como a componente do vetor é negativo, vamos descrevê-lo com um ângulo calculado no sentido horário a partir do semieixo horizontal positivo:
Passo 3
Agora vamos calcular o momento total dessas forças em relação ao ponto . Para isso temos que multiplicar cada componente de cada força pela sua distância perpendicular até esse ponto.
Começando pela força de , apenas a sua componente vertical vai produzir momento:
A força de é totalmente vertical, então seu momento é dado por:
E a força de é totalmente horizontal, mas favorece a rotação no sentido anti-horário, então aparee com sinal positivo:
Então o momento total é:
Onde o sinal negativo indica que o momento favorece a rotação no sentido horário.
Isso quer dizer que, se aplicarmos um momento de sobre o sistema, podemos substituir todas as três forças pela força que calculamos aplicada sobre o ponto .
Resposta
O sistema pode ser substituído por uma força de módulo a um ângulo de no sentido horário com o semi-eixo horizontal postivo aplicada no ponto , e um momento de módulo no sentido horário.