0 tripe mostrado na Figura 1.64 e usado para montar um instrumento eletrônico que determina a distância entre dois pontos no espaço. As hastes de apoio do tripe estão localizadas simetricamente em relação ao ponto media do eixo vertical. Se cada uma haste de apoio tiver um comprimento e rigidez axial , determine a rigidez equivalente do tripé do sentido vertical.
Passo 1
Para o item b, temos que:
Seja = deslocamento vertical de massa M, = deformação resultante de cada mola inclinada.
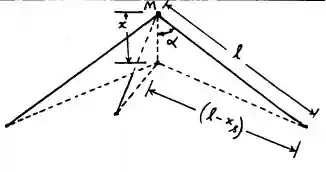
Da equivalência de energia potencial, temos:
Passo 2
Pela geometria, temos que:
Resolvendo a equação acima:
Usando a relação , podemos reescrever a equação acima novamente:
Assumindo ser pequeno, podemos simplificar de forma que:
De uma maneira similar,