A Figura 1.67 mostra uma mola de ar. Esse tipo de mola costuma ser usado para obter frequências naturais muito baixas e, ao mesmo tempo, manter deflexão zero sob cargas estáticas. Determine a constante elástica dessa mola de ar admitindo que a pressão e o volume mudam adiabaticamente quando a massa se move.
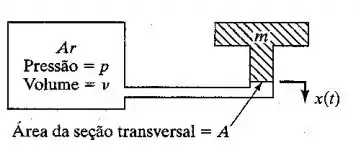
Passo 1
Saalve, tudo certo? Bora pra questão! Temos que:
A diferenciação dessa equação acima nos dá:
Mudança no volume quando a massa se move por .
Passo 2
Relacionando essas equações temos:
A força devido a mudança de pressão
Constante da mola devido ao ar: