Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 56

Um triturador de pedras consiste de um disco fino grande que está cconectado por pino a um eixo horizontal. Se o eixo gira a uma taxa constante de 8 rad/s, determine a força normal que o disco exerce sobre as pedras. Suponha que o disco rola sem deslizar e tenha uma massa de 25 kg. Despreze a massa do eixo.

Passo 1

Começaremos o exercício calculando os momentos de inércia com relação ao eixos principais:

I x = I z = 1 4 25 0,2 2 + 25 0,8 2 = 16,25   k g . m 2

I y = 1 2 25 0,2 2 = 0,5   k g . m 2

Passo 2

Agora iremos escrever a velocidade angular em termos das componentes:

ω = - ω y j + ω z k

Sabendo que ω z = 8   r a d / s , sendo assim:

v = 0,8 ω z = 0,8 8 → v = 6,4   m / s

ω y = - 6,4 0,2 → ω y = - 32   r a d / s

Passo 3

Agora iremos aplicar a equação da aceleração angular para o sistema com o auxílio do diagrama a seguir:

ω ˙ = ω ˙ x y z + Ω × ω = 0 + 8 k × - 32 j + 8 k = 256 i

ω x = 256   r a d / s 2

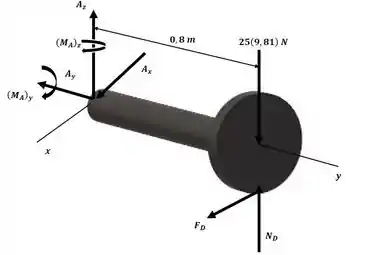
Agora iremos aplicar o somatório de momento para o eixo x, ainda com o auxílio do diagrama anterior:

∑ M x = I x ω x - I y - I z ω y ω z

N D 0,8 - 25 9,81 0,8 = 16,25 256 - ( 0,5 - 16,25 ) ( - 32 ) ( 8 )

N D = 405   N

Resposta

N D = 405   N

Ver Outros Exercícios desse livro