Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 37
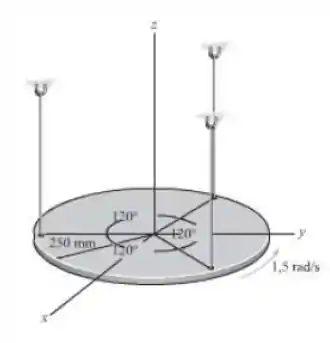
A placa tem uma massa de 10 kg e está suspensa por cordas paralelas. Se a placa tem uma velocidade angular de 1,5 rad/s em torno do eixo z no instante mostrado, determine até que altura o centro da placa sobe no instante que a placa momentaneamente para.
Passo 1
Temos um problema de cinética de corpo rígido. Problemas deste tipo requerem muito cuidado para não errarmos uma pequena conta ou esquecermos algum parâmetro.
Este problema é bem mais simples do que ele aparenta ser. É um problema de conservação de energia. No início, ele possuía apenas energia cinética, dada por:
Após ele subir, chegará um momento em que ele irá parar de rodar. Neste exato momento, ele só possuirá energia potencial gravitacional, a qual é dada por:
Portanto, como há conservação de energia, temos:
Sendo assim, cabe a nós calcularmos cada um dos parâmetros com muita calma para não errarmos!
Passo 2
Vamos calcular a energia cinética inicialmente. Para isto, precisamos determinar o momento de inércia em torno do centro de massa do nosso disco. Logo,
Agora, aplicando este valor na equação da energia cinética, temos:
Passo 3
Agora, para descobrirmos a altura que o disco sobe, basta aplicarmos a equação da conservação de energia. Logo,