Usando as equações AISC, verifique se a coluna que tem a seção transversal mostrada na figura pode suportar uma força axial de 1.500 kN. A coluna tem comprimento de 4 m, é feita de aço A-36 e suas extremidades estão presas por pinos.
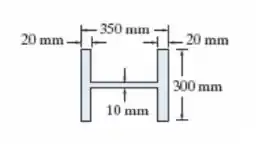
Passo 1
Extremidades presas por pinos,
Primeiramente, vamos determinar o momento de inércia e a área:
Agora, podemos calcular o
Com isso, podemos determinar o limite do índice de esbeltez:
Logo, verificando-se:
Como é menor que o limite, está ok.
Passo 2
Vamos agora verificar se P admissível é maior que o limite de 1500kN.
Resolvendo essa expressão, teremos:
Logo, a coluna é adequada, pois atende às especificações de carga crítica e índice de esbeltez.
Resposta
A coluna é adequada.