Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 48

Usando o método da seção 5.2, resolva o problema 5.15.

Passo 1

Fala aí, galerinha. Tudo bem com vocês? Bora estudar mais.

Este problema nos pede para determinar a tensão normal máxima na seção a - a , utilizando o método pedido.

Primeiramente, devemos determinar as reações de apoio. O DCL é:

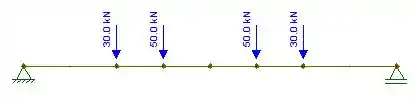
Por simetria, sabemos que:

F A = F B = 50 + 50 + 30 + 30 2 = 80   k N

Agora, basta calcular o momento na seção pedida:

M a - a = 80 × 2 - 30 × 1,2 - 50 × 0,4 = 104   k N m

Passo 2

Agora, basta calcular a tensão. Sabemos que:

σ = M S

Onde M   é o momento calculado e S   é uma propriedade da seção, que é tabelada. Usando a tabela no final do livro:

S = 747 × 10 - 6 m 3

Logo:

σ = M S = 104 × 10 3 747 × 10 - 6 = 139,2   M P a

Pronto, mais uma questão resolvida.

Resposta

σ = 139,2   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Trace os diagramas de força cortante e momento fletor para a viga e carregamento mostrados e, determine a tensão normal máxima provocada pelo momento fletor.
Usando o método da Seção 5.2 , resolva o Problema 5.20 .Para a viga e o carregamento mostrados, determine a tensão normal máxima provocada pelo momento fletor na seção transversal C .
Trace os diagramas de força cortante e momento fletor para a viga e carregamento mostrados e, determine a tensão normal máxima provocada pelo momento fletor.
Determine ( a ) as equações das curvas de força cortante e momento fletor para a viga e o carregamento mostrados na figura e ( b ) o valor máximo absoluto do momento fletor na viga.
Trace os diagramas de força cortante e momento fletor para a viga e carregamento mostrados e, determine a tensão normal máxima provocada pelo momento fletor.