Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 110
O vão central da ponte George Washington, tal como foi originalmente construída, consistia em um tabuleiro uniforme sustentada por cada cabo era ao longo da horizontal. Sabendo que o vão é e que a flecha é , determine, para a configuração original, (a) a tração máxima em cada cabo, (b) o comprimento de cada cabo.
Passo 1
Bom galera, vamos começar esboçando o cabo pra facilitar nossa vida, fica mais ou menos assim:
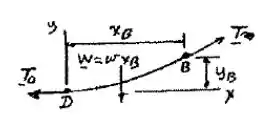
Onde sabemos que:
Logo:
Passo 2
Show de bola, agora a gente calcula o peso , isso é fácil, é assim:
Já que já temos isso a gente pode fazer simplesmente um Pitágoras para encontrar a tração máxima no cabo, bora lá:
Passo 3
Por fim, calculamos o comprimento do cabo com Equação do livro que é:
Que converge para:
Resposta
Exercícios de Livros Relacionados
Para o carregamento na viga determine (a) os diagramas de momento fletor e cortante e (b) os valores absolutos máximos de momento fletor e esforço cortante.
Se a reação é uniformemente distribuída no solo e P = w a , determine (a) os diagramas de cortante e momento fletor e (b) os valores máximos absolutos de momento e cortante.
Trace os diagramas de cortante e momento fletor e (a) determine os esforços imediatamente a esquerda de C e (b) imediatamente a direita.
Se a reação é uniformemente distribuída no solo, determine (a) os diagramas de cortante e momento fletor e (b) os valores máximos absolutos de momento e cortante.
Se a reação é uniformemente distribuída no solo, determine (a) os diagramas de cortante e momento fletor e (b) os valores máximos absolutos de momento e cortante.