Uma viga de aço de de comprimento suporta uma massa de em sua extremidade livre, como mostra a Figura 2.76. Determine a frequência natural de vibração transversal da massa modelando-a como um sistema com um grau de liberdade.
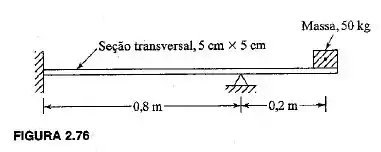
Passo 1
Queremos a frequência natural do sistema dado na figura do enunciado.
A frequência natural é dada por:
Temos que encontrar a rigidez equivalente .
Para o sistema dado, temos que:
Onde é a equação para deflexão no ponto devido a carga. Para saber o modo desta equação você pode analisar o apêndice que diz respeito à “deflexão das vigas e placas” e obter a seguinte fórmula para o sistema:
Temos que e . Como queremos saber a equação aplicada ao ponto onde a massa está agindo, temos que:
Passo 2
Substituindo na equação, temos que:
Desenvolvendo, temos que:
Temos que o momento de inércia da viga é dado por:
Nos foi dito que a viga tem seção transversal quadrada de , portanto, e .
Temos que:
Passo 3
Portanto, a rigidez equivalente do sistema será:
Substituindo os valores, temos que:
Podemos finalmente descobrir a frequência natural do sistema: