Derive a equação de movimento do sistema mostrado na figura 2.73. com a utilização dos seguintes métodos:
- Segunda lei do movimento de Newton;
- Princípio de D’Alembert;
- Princípio do trabalho virtual;
- Princípio da conservação da energia.
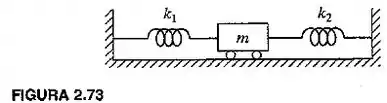
Fonte: Rao Vibrações Mecânicas – 4ª ed
Passo 1
Olá meus pimpolhos!
Bora dar continuidade à temida Vibrações haha!
Enfim, esse problema basicamente quer nos fazer lembrar de conceitos importantes para diferentes maneiras de encontrar a equação do movimento.
Vamos lá relembrar cada método!
Passo 2
Letra a) Devemos nos lembrar que a segunda Lei de Newton nos diz que o somatório de todas as forças do sistema em movimento é igual ao produto da massa pela aceleração do sistema, assim:
Passo 3
Letra b) O princípio de D’Alembert afirma que a soma das diferenças entre as forças que agem sobre o sistema e suas derivadas no tempo é zero, assim:
Ou
Passo 4
Letra c) O princípio do trabalho virtual nos fala que “é nulo o trabalho realizado ao longo de um deslocamento virtual infinitesimal arbitrário de um sistema, a partir de uma posição de equilíbrio.”
Em outras palavras, o trabalho virtual total realizado por todas as forças deve ser igual a zero, assim:
Passo 5
Letra d) Por fim, temos o princípio da conservação da energia, que nos diz que, comparando dois instantes, a energia total(mecânica) de um instante deve ser igual a energia total do outro instante analisado.
Então, nesse sistema temos energia cinética e potencial elástica. De acordo com o que foi dito anteriormente, o somatório dessas energias deve ser uma constante, então:
Aplicando a derivada nos dois lados:
Assim, temos:
Resposta
Portanto, foram aplicados os métodos que chegaram a um único valor em comum: