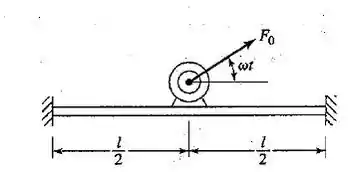
Uma viga de aço fixa dos dois lados, com de comprimento, de largura e de espessura, suporta um motor elétrico de de massa e velocidade rpm no meio do vão, como mostra a Figura 3.56. Uma força rotativa de magnitude e desenvolvida devido ao desequilíbrio do rotor do.motor. Determine a amplitude das vibrações em regime permanente desconsiderando a massa da viga. Qual será a amplitude se a massa da viga for considerada?
Passo 1
(a)
A amplitude da vibração em estado estacionário é dada pela Eq. (3,30) com :
Passo 2
(b) Usando a massa efetiva devido ao peso próprio da viga (para um cantilever) para ser válido aqui também,
onde M = mastro do motor = 75 "" kg, e m = massa da viga = (