Solução de Grelhas Compostas
Produzido por Pablo RicardoTeoria
Introdução
O objetivo dessa aula é entendermos como sairemos de uma grelha composta, para diversas grelhas simples. É importante que não nós concentraremos em resolver as grelhas simples já que já aprendemos a fazer isso na aula de solução de grelhas simples. O objetivo é passar o passo a passo para aprendermos como resolver uma grelha composta. Para fazer isso temos que fazer o seguinte
- Achar todas as rótulas e dobradiças, pois serão possíveis pontos de quebra para analisarmos grelhas simples
- Quebrar essas rótulas e dobradiças e substituir por apoios fictícios
- Analisar se as treliças formadas são simples e isostáticas
- Definir o melhor apoio para estrutura (alguns professores deixam um apoio faltando e pedem para o aluno dizer qual seria o melhor apoio para aquela estrutura)
- Pegar todas as reações de apoios fictícios e transferir para as barras em que eles se apoiam
- Definir uma ordem de solução
- Calcular as reações de apoio
- Calcular os diagramas
Visto todos esses passos, vamos ver um exemplo, e a partir desse exemplo vamos entender melhor como resolver esse tipo de questão.
Situação
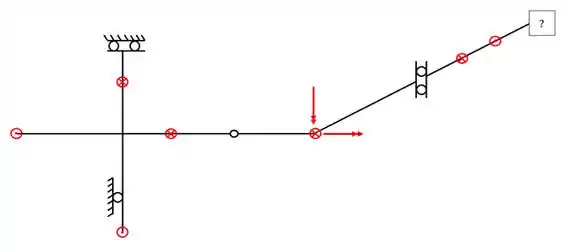
Imagine que na sua prova cai exatamente essa grelha para você resolver. E o seu professor pergunte o seguinte
- Qual o melhor apoio para colocar no ponto de interrogação?
- Qual a divisão das grelhas simples?
- Qual as equações de momento e cortante, assim como os seus diagramas?

Parece que é muito complicado né? Por isso vamos ver um passo a passo que vai deixar tudo muito mais simples, vamos lá então.

Passo 1: achar as rótulas e dobradiças, quebrar elas e substituir por apoios fictícios.
Como já vimos na aula de conceitos de grelhas, já sabemos que apoios colocar quando quebramos as rótulas, com isso, na nossa grelha teremos que
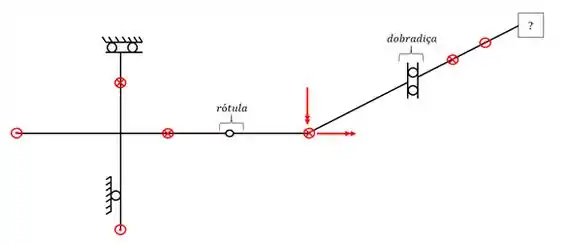
Identificado as rótulas e dobradiças, podemos quebrar elas e colocar os apoios fictícios e passaremos as ter
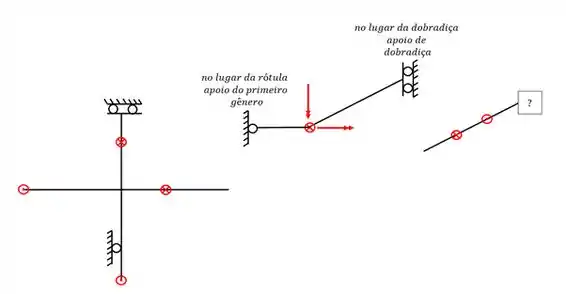
Perceba que a grelha mais a esquerda possui um apoio do primeiro gênero e um apoio de dobradiça, ao todo, 3 incógnitas. Como ela não possui rótulas, temos 3 equações de equilíbrio. Logo, temos 3 incógnitas e 3 equações, logo, uma grelha simples e isostática.
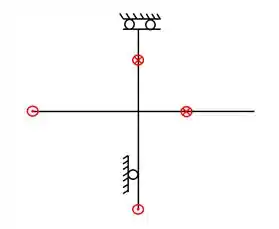
A grelha central também possui um apoio do primeiro gênero e um apoio de dobradiça, sendo ao todo, também 3 incógnitas. Como ela não possui rótulas, temos 3 equações de equilíbrio. Logo, temos 3 incógnitas e 3 equações, logo, também é uma grelha simples e isostática.
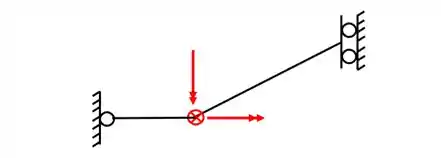
Por fim, a grelha a direita não possui nenhum apoio, e queremos que ela seja isostática, a única forma disso acontecer é se essa grelha possui um apoio de engaste, pois como ela não possui rótulas, ela tem 3 equações, logo, precisa de 3 incógnitas, e dessa forma, a nossa grelha será
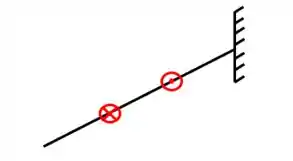
Assim respondemos a primeira pergunta que era qual o melhor apoio a ser colocado no ponto de interrogação.
Passo 2: trocar os apoios pelas reações de apoio e definir para onde cada reação de apoio fictício irá.
Nesse caso vamos diferenciar a cor dos apoios fixos e dos apoios fictícios. Trocando os nossos apoios teremos
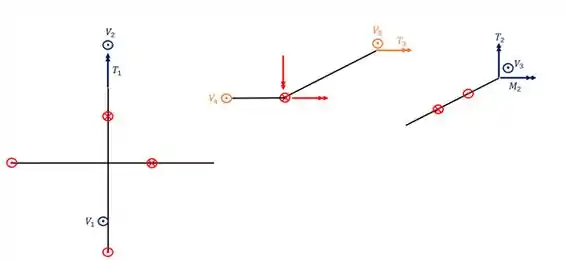
Todas as reações de apoios em azul são fixas, ou seja, não serão transferidas para outras grelhas. As reações de apoio em laranja marcam as reações de apoios fictícios, ou seja, que serão transferidos para outras grelhas. Mas como faremos essa transferência?
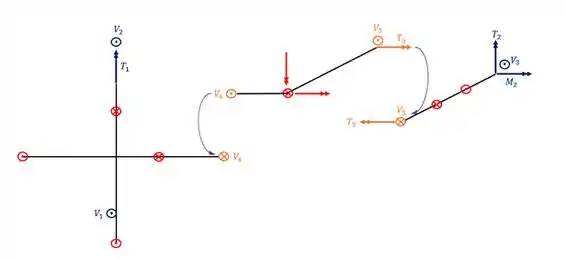
Perceba que a transferência ocorreu dos apoios fictícios para as grelhas em que esses apoios se apoiam, o que vale destacar?
- A grelha do meio transferiu carregamento para as outras duas grelhas
- Todas as reações dos apoios fictícios foram transferidas para as grelhas com o sinal contrário
- Perceba que usamos a representação usual de grelhas pra indicar que invertemos o sentido dos vetores.
Com isso já podemos definir a ordem de solução da nossa grelha.
Passo 3: definir a ordem de solução, calcular as reações de apoio e desenhar os diagramas
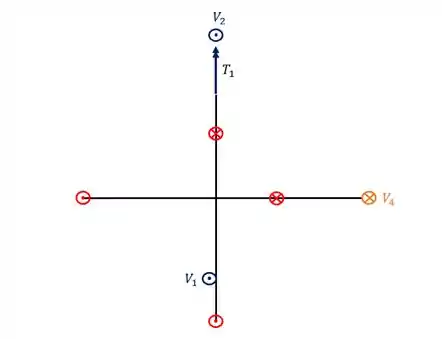
A primeira grelha a ser resolvida, tem que ser a grelha mais externa, que possua apenas apoios fictícios, e que não recebe nenhum apoio fictício de outra grelha. A única barra que passa por todos esses testes é a barra central, logo, na nossa ordem de solução ela será a primeira a ser resolvida, lembrando que resolver uma grelha consiste em definir as reações de apoio e desenhar os diagramas, com isso resolveremos primeiro
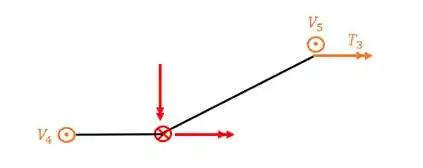
A segunda grelha a ser resolvida é a da esquerda. Essa escolha é estratégica pois essa grelha possui reações de apoio mais simples, dessa forma, poderemos calcular ela. Vale relembrar que devemos considerar a contribuição da rótula que calculamos na grelha anterior, lembrando sempre de inverter o sentido do vetor. Dessa forma nossa segunda grelha a ser resolvida, determinando as suas reações de apoio e diagramas é
Por fim falta apenas a ultima grelha a ser resolvida, que também terá contribuições da barra do meio. Nesse caso iremos transferir com o sentido contrário do calculado para as reações de apoios fictícios e teremos a seguinte grelha
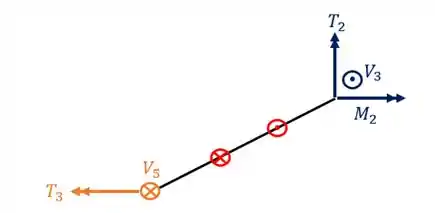
Veja que a partir dela conseguimos determinar reações de apoio, diagrama de momentos fletores e cortantes, dentre outros diagramas que forem pedidos.
Com isso conseguimos determinar tudo que o nosso professor pedia na questão, assim como todas as características iniciais que foram dadas na introdução. Esse passo a passo mais a aula de solução de grelhas simples vai te tornar um craque dos exercícios.
Bora solucionar os problemas, exercícios e questões que podem cair na sua prova? Vamos lá treinar nos exercícios.
