Avaliação do Modelo
Teoria
Criamos um modelo linear para relacionar duas variáveis... Mas como sabe se esse modelo é adequado? Como saber se está bom ou se viajamos?
Pra isso temos algumas forma de analisar :D
- Estimador de
- Decomposição da Soma de Quadrados
- Análise de Variância pela tabela ANOVA.
Calma que vamos ver direitinho cada um!
- Estimador de
- Decomposição da Soma de Quadrados
- Análise de Variância pela tabela ANOVA.
Para julgarmos a adoção de um modelo mais complexo, vamos compara-lo a um modelo mais simples.
O modelo mais simples a ser utilizado é o:
A vantagem será sempre medida por meio da diminuição dos erros de previsão, ou ainda, pela variância residual.
Para tal modelo, cada resíduo é dado por:
Lembrando que resíduo é a soma de todos os errinhos de outros fatores (além da nossa variável independente) que influenciam na nossa variável dependente.
E lembre-se que é o valor ESTIMADO, ou seja, vamos utilizar o que encontramos pela fórmula anterior, enquanto é o valor amostral.
Continuando....
Podemos olhar esse resíduo de várias formas para então determinar se ele é um bom representante dos verdadeiros desconhecidos.
Porém olhar eles de forma independente da muito trabalho então procuramos um jeito de juntá-los, e esse jeito é o SQRes. Mas o que é este SQRes?? Eu te respondo, é a soma quadrada dos resíduos:
Mas pequeno quanto? Temos que compará-los com algo e esse é o SQTot, soma dos quadrados totais, e quem é ele?
Sabemos também que a variância amostral S² ou se dá pela seguinte fórmula:
Porém quando estimamos , perdemos mais um grau de liberdade.
E como todos sabemos que a variância amostral é um estimador não viesado da variância populacional, isto é, , tchanam achamos nosso estimador!! A raiz quadrada deste , ou seja, é chamado de erro padrão da regressão.
Ao passarmos do modelo simples para o modelo de regressão linear, vimos que a soma de quadrados é dada por:
Resultando no que chamamos Soma de Quadrados devida à Regressão.
Mas quem são esses caras??
Mas para que servem essas somas, elas servem para testar se o modelo está “bom”, e como analisamos?? Simples o ideal seria que a SQRes fosse 0, pois não teriam erros na minha regressão, porém isso é impossível então nós esperamos que ele seja o menor possível.
Podemos resumir todas as informações anteriores numa única tabela, chamada de ANOVA. Essa tabela segue o seguinte modelo:
Onde:
Podemos assim verificar qual o ganho relativo ao escolher tal modelo, usando a estatística:
O que diz esse R²? Ele diz o quanto da minha do meu SQTot é explicado pelo meu SQReg, ou seja, quanto maior esse valor melhor é a minha regressão, pois quase nada dela está sendo explicado pelos erros.
Simples assim? SIMPLES ASSIM, mano o R² varia de 0 a 1, se ele tiver muito próximo do 1 BUM!, a regressão não tem quase nada de erro! (veremos depois que ainda faltam outros testes para garantir uma boa regressão, mas vitórias são para serem comemoradas)
Ah, guarda aí a quinta coluna que depois falaremos melhor sobre ela!
Exercícios Resolvidos
Exercício Resolvido #1
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 6
Um estudo sobre duração de certas operações está investigando o tempo requerido (em segundos) para acondicionar objetos e o volume (em ) que eles ocupam. Uma amostra foi observada e obtiveram-se os seguintes resultados:
a) Faça o diagrama de dispersão dos dados.
b) Estime a reta de regressão do tempo de operação em função do volume.
c) Construa a tabela ANOVA para o modelo.
d) Qual o valor de ? É pequeno quando comparado a
e) Você acha que conhecer o volume do pacote ajuda a prever o tempo de empacotamento?
Passo 1
Neste exercício precisaremos ter muita atenção pois aplicaremos quase tudo que vimos, montar o gráfico dos pares de dados, estimar a reta de regressão e montar a tabela anova!
Passo 2
Para montar o gráfico pegamos os pares de dados e plotamos eles, mais ou menos assim
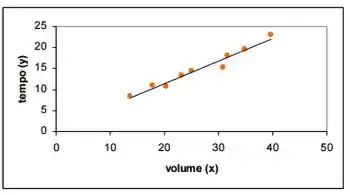
Passo 3
Agora para a letra b precisamos estimar os valores para α e β, só aplicar a fórmula de minímos quadrados, caso você esteja com alguma dificuldade nessa parte recomendo que revise a teoria 1 deste tópico, mas atente-se em que você escolhe como x e y.
A reta será
Passo 4
Na letra C é que teremos trabalho, para montarmos a tabela ANOVA vamos precisa lembrar algumas coisas, tais como
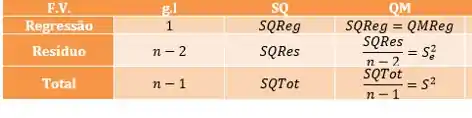
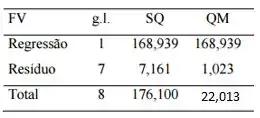
Passo 5
Para resolver esta letra basta checarmos a tabela anova pra ver que e . E assim é possível perceber que é realmente pequeno comparando um ao outro.
Passo 6
Após todas as análises que fizemos, podemos sim concluir que conhecer o volume do pacote ajuda a prever o tempo de conhecimento, isto é, a regressão é significativa.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 20
A análise do lucro anual de uma ação, como função linear da dua cotação média anual, forneceu os resultados abaixo com alguns campos em branco. Preencha a lacuna e interprete os resultados.
Passo 1
Para essa questão precisamos apenas escrever os dados da tabela ANOVA que faltam, e dizer coisas sobre o modelo como os QMRes é bem menor que QMTot ou não.
Passo 2
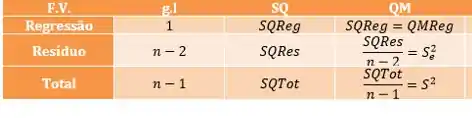
Olhando para a tabela vemos que faltam
Agora é só colocar os valores na tabela.
- "Conseguimos perceber que o QMREs é bem menor que o QMTot, isso da uma boa ideia que a regressão é significativa.
"Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 1
Passo 1
No exercício precisamos calcular a reta dos mínimos quadrados, e depois achar o SQRes/n-2
Passo 2
Se você ainda tem dificuldades para calcular a reta por mínimos quadrados, recomendo que de uma olhada na teoria 1 deste módulo.
Temos a reta
Passo 3
Para acharmos o erro padrão da estimativa o primeiro passo é achar SQRes
Agora basta dividir por n-2 que acharemos
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 1
Construa a tabela Anova para os dados e interprete:
Passo 1
No exercício precisamos calcular a tabela ANOVA, e interpretar resultados como significância da regressão:
Passo 2
Para começarmos precisamos achar os estimadores dos parâmetros, se você tem dificuldade com isso de uma relembrada na parte de mínimos quadrados. A reta é:
Passo 3
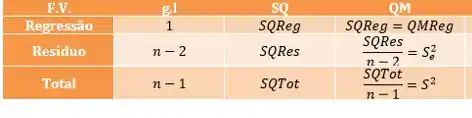
Agora completando os dados que faltam da tabela (no caso todos)
Passo 4
Podemos ver que o é bem menor que o , e isso indica uma regressão bem significativa.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 1
Construa a tabela Anova para os dados:
Passo 1
No exercício precisamos encontrar a tabela ANOVA, e interpretar resultados como significância da regressão:
Passo 2
Para começarmos precisamos achar os estimadores dos parâmetros, se você tem dificuldade com isso de uma relembrada na parte de mínimos quadrados. A reta é:
Passo 3
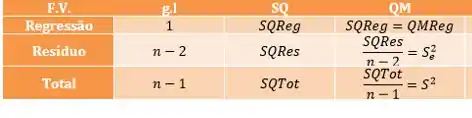
Agora completando os dados que faltam da tabela (no caso todos)
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 1
- Determine a estimativa da linha de regressão do número de erros em função do número de horas sem dormir.
- Construa uma tabela ANOVA
- Ache o R² e interprete
Passo 1
No exercício precisamos encontrar, a reta de regressão, tabela ANOVA, e interpretar alguns resultados como significância da regressão por exemplo:
Passo 2
Para resolvermos a letra A precisamos achar os estimadores dos parâmetros, se você tem dificuldade com isso de uma relembrada na parte de mínimos quadrados. A reta é:
Passo 3
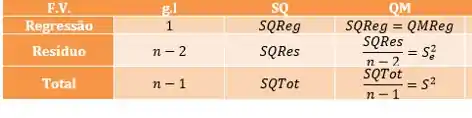
Agora para resolvermos a letra B precisamos completar os dados que faltam da tabela (no caso todos)
Passo 4
Para calcular a letra d, vamos calcular o R², que tem a fórmula
Um pouco acima de 50%, porém não é tão bom assim
Resposta
Ei, a resposta está no passo a passo :)