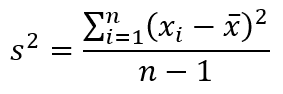Fórmula da Variância Amostral
Resumo
Fala aí, nós somos o Responde Aí, e nossa missão é ajudar você a mandar bem na sua prova.
A Variância Amostral é uma medida de dispersão que expressa o quanto os valores de um conjunto de dados estão distantes da média.
A fórmula da variância amostral é:
Entendendo melhor cada item da fórmula da variância amostral:
é a nossa variância amostral; é cada um dos dados pertencentes ao conjunto; é a média dos dados do conjunto; é a quantidade de dados desse conjunto
Importante: A unidade que expressamos a variância amostral é o quadrado da unidade dos dados do conjunto. Por exemplo, se os dados do conjunto são expressos em cm a variância amostral será expressa em cm2, show de bola?
Pra que serve?
A variância amostral nos fornece o quanto um conjunto de dados está distante do valor médio, ou seja, dá uma ideia do quanto os dados são homogêneos, beleza?
Pra fórmula da variância amostral ficar presa na sua cabeça, a melhor forma é ver um exemplo!
Exemplo:
Imagina que a altura, em metros, de cinco pessoas, dentro de uma sala, sejam as seguintes:
Calcule a variância amostral desse conjunto de alturas?
Passo 1: Calcule a média dos dados. Temos cinco dados na lista acima. Então, é só a gente somar tudo e dividir por
Passo 2: Aplique a fórmula da variância amostral
logo:
E é só isso! Viu que da hora! Então dá mais uma olhada na fórmula da variância amostral pra não esquecer: