Alguém sugere que, no teste de hipóteses, é possível eliminar um erro tipo I fazendo-se . Em um teste bilateral, que valores críticos correspondem a ? Se , a hipótese nula pode ser rejeitada?
Passo 1
Tudo certo, gente? Vamos explorar um pouco o que aconteceria se o nível de significância () for zero. Vamos ter que usar uma tabela de distribuição normal de novo! Aqui embaixo, trouxe uma imagem de uma tabela dessas!
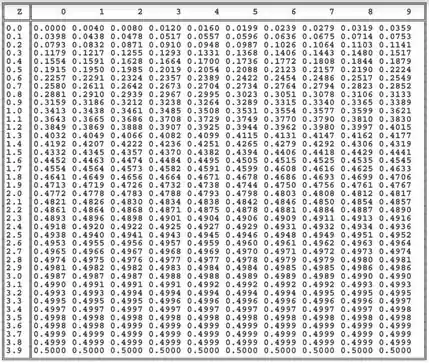
Primeiro, vamos procurar o valor de Z referente ao informado. Como o teste é bilateral, vamos dividir por 2, o que ainda nos daria um valor de 0. Agora temos que achar o valor (entre os do meio da tabela) mais próximo de . Nesse caso, vemos na tabela que a última linha inteira tem valor de 0,5000, então vamos pegar a primeira coluna. Beleza! Agora é só montar o Z com as informações da linha e depois da coluna da tabela. Fica assim:
3,9 (linha) e 0 (coluna) Z = 3,90
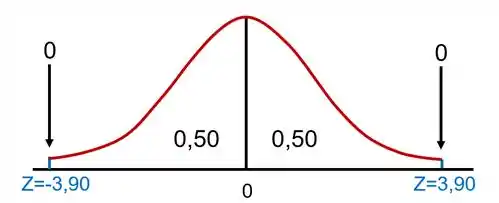
Então teremos, para um teste bilateral, os valores críticos Z = -3,90 na esquerda e Z = 3,90 na direita.
Passo 2
Show! Agora que temos o Z, vamos pensar! Será que a hipótese nula poderia ser rejeitada nessa situação? Se antes dividíamos um gráfico entre a porção e , agora percebemos que teríamos que dividir as duas metades entre 0,5 e 0, ou seja, não seria possível cair em um espaço em que fosse possível rejeitar , já que a região de rejeição seria nula.
E pronto! Acabamos! Simples, né?
Resposta
Valores críticos: Z = -3,90 e Z = 3,90.
Se , a hipótese nula não pode ser rejeitada.