Suponha o leitor que esteja trabalhando com um nível de significância para testar a hipótese , e que sua amostra consista em 50 valores selecionados aleatoriamente. Determine a probabilidade de cometer um erro tipo II, dado que a população tem efetivamente distribuição normal com e . (Sugestão: Com : , comece determinando os valores das médias amostrais que não levem à rejeição de ; ache em seguida a probabilidade de obter uma média amostral com um daqueles valores.)
Passo 1
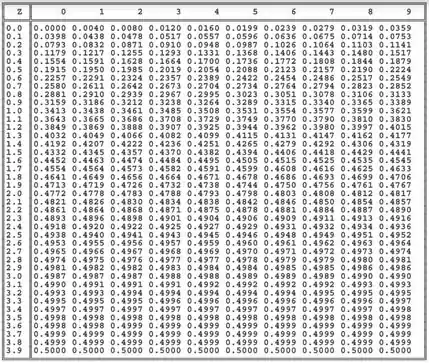
Tudo certo, galera? Vamos pro último exercício dessa seção! Agora vamos montar um exercício de teste de hipótese de fato. Vamos ter que usar uma tabela de distribuição normal de novo! Aqui embaixo, trouxe uma imagem de uma tabela dessas!
Também vamos precisar usar a fórmula do Z para um Teste de Hipóteses para média (com conhecido ou ):
Primeiro, vamos determinar os valores iniciais do problema, montando e (já sabemos que o teste será unilateral esquerdo porque vamos testar a hipótese ):
Passo 2
Agora temos que encontrar o Z a partir da fórmula para :
Em seguida, chegamos ao valor de correspondente ao Z encontrado na tabela, já que buscamos a seguinte situação:
Buscando os primeiros algarismos entre as linhas e o último entre as colunas. Assim, percebemos que, ao procurar por Z=3,54, encontramos .
Passo 3
Sendo assim, como estamos procurando a probabilidade de ocorrer um erro tipo II, ou seja, não rejeitar , sendo falsa, com um nível de significância e , não seria possível não rejeitar , já que o valor é menor que , então o valor cairia dentro da Região de Rejeição de .
E pronto! Acabamos! Simples, né?
Resposta
A possibilidade de um erro tipo II é nula.