No exercício 17, determine o menor valor da média amostral acima de $40.000 que apoie a afirmação de que a média é superior a $40.000. (Use o mesmo tamanho de amostra e o mesmo desvio-padrão.)
Passo 1
Tudo certo, pessoal? A gente vai fazer agora mais um exercício que explora um caminho diferente de olhar os testes e hipótese, mas não é nada que não vamos conseguir fazer! É só repetir o processo que estávamos fazendo e alterar um pouquinho! Vamos ter que usar uma tabela de distribuição normal de novo! Trouxe aqui uma imagem dela pra vocês!
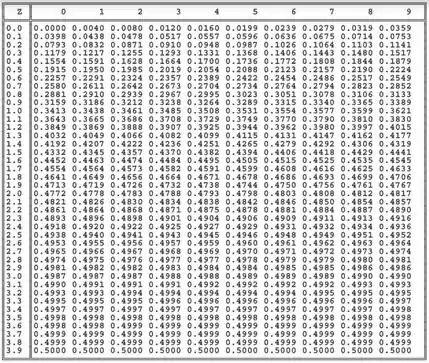
Também vamos precisar usar a fórmula do Z para um Teste de Hipóteses para média (com conhecido ou ):
Primeiro, vamos determinar os valores iniciais do problema, montando e (já sabemos que o teste será unilateral direito porque vamos testar a hipótese ):
Passo 2
Show! Agora vamos pensar: procuramos o menor valor de para que seja rejeitada com um nível de significância . Ou seja, e, consequentemente, por ser um teste unilateral direito, quer dizer que o valor da tabela Z correspondente deve ser menor que:
Ou seja, buscando na tabela, procuramos um (fazendo média das colunas 7 e 8 para o dígito final), que representa o limite de Z do problema.
Passo 3
Tá quase! Agora, usamos a fórmula de Z para chegar em :
Sendo assim, o valor limite de média amostral encontrado é , ou seja, a menor média amostral possível para representar essa situação é de .
E pronto! Acabamos! Simples, né?