Enunciado
Probabilidade e Estatística - Triola - Introdução à Estatística- Ed: 7º - Capítulo 7.6 - Ex. 6
As alturas dos homens variam mais do que as das mulheres? A enfermeira de um colégio feminino coletou dados de exames físicos. As alturas das mulheres acusaram um desvio-padrão de 2,5 in. O colégio agora tornou-se misto e os primeiros 20 estudantes de sexo masculino têm alturas com desvio-padrão de 2,8 in. Ao nível de significância de 0,025, teste a afirmação de que as alturas dos homens variam mais do que as das mulheres. Se a afirmação não for consistente, significa que a altura dos homens não variam mais do que as das mulheres?
Passo 1
Fala ae, pessoal! Bora fazer esse exercício de teste de hipóteses!
Seguindo o procedimento padrão para o teste de hipóteses, primeiro vamos dizer qual é a nossa hipótese nula e a nossa hipótese alternativa nesse problema:
Onde é a nossa hipótese original.
Passo 2
Como a afirmação é sobre um desvio-padrão, vamos aplicar a distribuição qui-quadrado.
Dando uma olhada na hipótese dada, vemos que o teste realizado será unilateral direito, então vamos ter apenas um valor crítico, na cauda direita.
O valor crítico vai ser o valor mostrado na tabela da distribuição qui-quadrado para:
Então, o valor crítico vai ser .
Passo 3
Vamos dar uma olhada no gráfico abaixo:
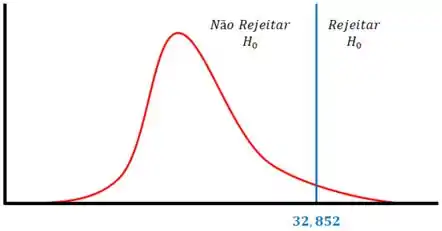
Como está fora da região crítica, não rejeitamos a hipótese nula .
Resposta
Não há evidência amostral para apoiar a afirmação de que as alturas dos homens variam mais do que as das mulheres. Isso não significa, necessariamente, que as alturas dos homens não variam mais do que as das mulheres, mas essa é uma possibilidade.