Enunciado
Probabilidade e Estatística - Triola - Introdução à Estatística- Ed: 7º - Capítulo 7.6 - Ex. 7
A Kansas Farm Products Company usa uma máquina que enche sacos de 50 lb de semente de milho. No passado, a máquina apresentava um desvio-padrão de 0,75 lb. Com o intuito de obter pesos mais compatíveis, os mecânicos substituíram algumas peças gastas da máquina. Uma amostra de 61 sacos, extraída da máquina já reparada, acusou média amostral de 50,13 lb e desvio-padrão amostral de 0,48 lb. Ao nível de 0,05 de significância, teste a suposição de que os pesos são “mais compatíveis” com a máquina reparada, em comparação com a situação anterior. Se os pesos são mais compatíveis, qual é o efeito sobre o desvio-padrão?
Passo 1
Fala ae, pessoal! Bora fazer esse exercício de teste de hipóteses!
Seguindo o procedimento padrão para o teste de hipóteses, primeiro vamos dizer qual é a nossa hipótese nula e a nossa hipótese alternativa nesse problema:
Onde é a nossa hipótese original.
Passo 2
Como a afirmação é sobre um desvio-padrão, vamos aplicar a distribuição qui-quadrado.
Dando uma olhada na hipótese dada, vemos que o teste realizado será unilateral esquerdo, então vamos ter apenas um valor crítico, na cauda esquerda.
O valor crítico vai ser o valor mostrado na tabela da distribuição qui-quadrado para:
Então, o valor crítico vai ser .
Passo 3
Vamos dar uma olhada no gráfico abaixo:
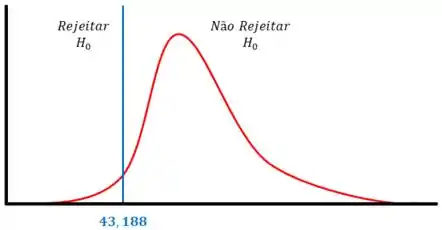
Como está dentro da região crítica, rejeitamos a hipótese nula .
Resposta
Os dados amostrais apoiam a afirmação de que o desvio-padrão diminuiu com o reparo, logo, os pesos ficaram “mais compatíveis”, pois variam menos.