Enunciado
Probabilidade e Estatística - Triola - Introdução à Estatística- Ed: 7º - Capítulo 7.6 - Ex. 5
Com filas separadas em cada um de seus vários guichês, o Jefferson Valley Bank constatou que o desvio-padrão das filas de espera, normalmente distribuídas, nas tardes de sexta-feira, era de 6,2 min. O banco experimentou trabalhar com uma fila única e verificou que, para uma amostra de 25 clientes, os tempos de espera têm um desvio-padrão de 3,8 min. Com base em estudos prévios, podemos admitir que os tempos de espera tenham distribuição normal. Ao nível de 0,05 de significância, teste a afirmação de que uma fila única apresenta menor variação dos tempos de espera. (Os clientes tendem a ficar mais satisfeitos se os tempos de espera apresentam menor variação.) A adoção de uma fila única resulta realmente em menor espera?
Passo 1
Fala ae, pessoal! Bora fazer esse exercício de teste de hipóteses!
Seguindo o procedimento padrão para o teste de hipóteses, primeiro vamos dizer qual é a nossa hipótese nula e a nossa hipótese alternativa nesse problema:
Onde é a nossa hipótese original.
Passo 2
Como a afirmação é sobre um desvio-padrão, vamos aplicar a distribuição qui-quadrado.
Dando uma olhada na hipótese dada, vemos que o teste realizado será unilateral esquerdo, então vamos ter apenas um valor crítico, na cauda esquerda.
O valor crítico vai ser o valor mostrado na tabela da distribuição qui-quadrado para:
Então, o valor crítico vai ser .
Passo 3
Vamos dar uma olhada no gráfico abaixo:
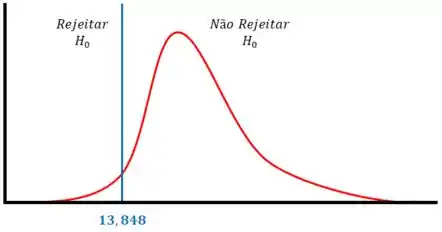
Como está dentro da região crítica, rejeitamos a hipótese nula .
Resposta
Os dados amostrais apoiam a afirmação de que uma fila única apresenta menor variação dos tempos de espera.