Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 2.3 - Ex. 63

Análise de dados. Um serviço de teste ao consumidor obteve as distâncias percorridas (em milhas por galão), mostradas na tabela a seguir, em cinco testes de desempenho com três tipos de carros compactos.

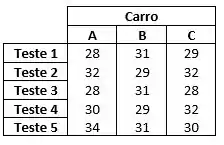
(a) O fabricante do carro A quer anunciar que seu carro teve o melhor desempenho no teste. Que medida da tendência central — média, mediana ou moda — deveria ser usada para essa afirmação? Explique seu raciocínio.

(b) O fabricante do carro B quer anunciar que seu carro teve o melhor desempenho no teste. Que medida da tendência central — média, mediana ou moda — deveria ser usada para essa afirmação? Explique seu raciocínio.

(c) O fabricante do carro C quer anunciar que seu carro teve o melhor desempenho no teste. Que medida da tendência central — média, mediana ou moda — deveria ser usada para essa afirmação? Explique seu raciocínio.

Passo 1

Calcular a média e a mediada do carro A:

Para o cálculo da média, utilizamos a seguinte equação:

x - =     ∑ x i n

Onde:

x i valores dados

n número de elementos do conjunto de dados

Temos que:

x - =     28 + 32 + 28 + 30 + 34 5 = 152 5

x - = 30,4

Para o cálculo da mediana, iremos construir o ROL em ordem crescente:

Como temos n = 5 , valor ímpar, então a mediana ( M e ) é o valor central do conjunto numérico:

M e = 3 0

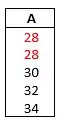
A moda é o valor que aparece com maior frequência:

M o = 28

Passo 2

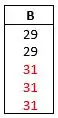
Calcular a média e a mediada do carro B:

x - =     ∑ x i n = 29 + 29 + 31 + 31 + 31 5 = 151 5

x - =     30,2

n = 5 , valor ímpar, então a mediana ( M e ) é o valor central do conjunto numérico:

M e = 3 1

M o = 31

Passo 3

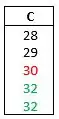
Calcular a média e a mediada do carro C:

x - =     ∑ x i n = 2 8 + 29 + 3 0 + 3 2 + 3 2 5 = 151 5

x - = 30,2

n = 5 , valor ímpar, então a mediana ( M e ) é o valor central do conjunto numérico:

M e = 30

M o = 3 2

Resposta

Carro A:

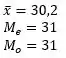
Carro B:

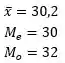
Carro C:

(a) Para afirmar que o carro A tem melhor desempenho é melhor utilizar a MÉDIA como medida de tendência central, porque o carro A é o que apresenta maior média entre os 3 carros.

(b) Para afirmar que o carro B tem melhor desempenho é melhor utilizar a MEDIANA como medida de tendência central, porque o carro B é o que apresenta maior mediana entre os 3 carros.

(c) Para afirmar que o carro C tem melhor desempenho é melhor utilizar a MODA como medida de tendência central, porque o carro C é o que apresenta o maior valor da moda entre os 3 carros.

Exercícios de Livros Relacionados

Encontrando a média ponderada - Nos exercícios 41 a 46, determine a média ponderada dos dados.41. Nota final - As notas, e seus percentuais na nota final, de um aluno de estatística são apresentados a
Encontrando a média ponderada - Nos exercícios 41 a 46, determine a média ponderada dos dados.42. Nota final - As notas, e seus percentuais na nota final, para um aluno de arqueologia são apresentadas
Nos exercícios 17 a 34, encontre a média, a mediana e a moda dos dados, se possível. Se quaisquer dessas medidas não puderem ser encontradas ou não representarem o centro dos dados, explique o porquê.
Nos exercícios de 37 a 40, sem realizar nenhum cálculo, determine qual medida de tendência central melhor representa os dados dos gráficos a seguir. Explique seu raciocínio38. Alturas (em polegadas) d
Nos exercícios 17 a 34, encontre a média, a mediana e a moda dos dados, se possível. Se quaisquer dessas medidas não puderem ser encontradas ou não representarem o centro dos dados, explique o porquê.