Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 1.Exercícios - Ex. 21
artigo citado no Exercicio 20 também forneceu os seguintes valores das variáveis números de sac e z = número de interseções:
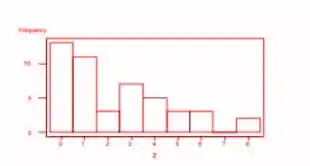
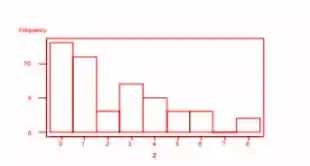
a. Construa um histograma dos dados de y. Que proporção dessas subdivisões não possuem culs-de-sac? Ao menos um cul-de-sac?
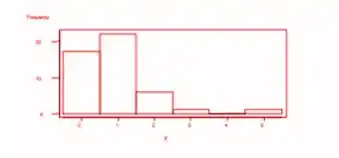
b. Construa um histograma para os dados z. Que proporção dessas subdivisões têm no máximo cinco interseções? Menos de cinco interseções?
Passo 1
a. Um histograma dos dados que aparece abaixo. A partir deste histograma, o número de subdivisões sem becos sem saída (ou seja, y=0) é 17/47=362, ou 36,2%. A proporção com pelo menos um cul-de-sac (y≥1) é (47-17)47=30/47=638, ou 63,8%. Observe que subtrair o número de becos sem saída com y=0 do total, 47 , é uma maneira fácil de encontrar o número de subdivisões com y≥1.
Passo 2
b. Um histograma dos dados z aparece abaixo. A partir desse histograma, o número de subdivisões com no máximo 5 interseções (ou seja, z≤5 ) é 42/47=894, ou 89,4%. A proporção com menos de 5 interseções (z
Resposta
