Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 13.Exercícios - Ex. 42

Um artigo na revista descreveu um experimente em que três métodos diferentes de preparar peixe são avaliados, com base no critério sensorial, sendo dada uma uma pontuação de qualidade. Considere que esses métodos tenham sido selecionados aleatoriamente a partir de uma grande população de métodos de preparação. Os dados estão na seguinte tabela:

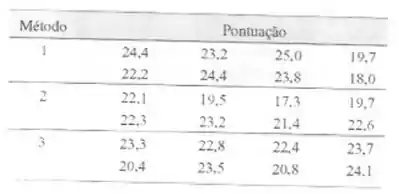
a)Há alguma diferença nos métodos de preparação? Use

b)Calcule o valor P para a estatística F no item (a).

c)Analise os resíduos provenientes do experimento e comente a adequação do modelo.

d)Estime os componentes de variância.

Passo 1

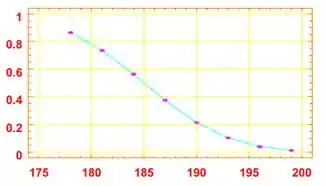
Hey, jovem, tudo bem contigo? Espero que sim 😊 Bora pra mais uma questãozinha de estatística? Vamo que vamo! Então, nessa questão a gente tem que para o item a), os resíduos vao se concentrar no gráfico da seguinte forma:

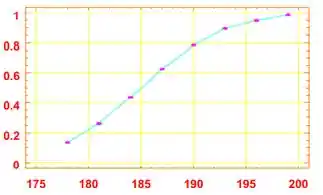
b) Para os resíduos contra y, temos o inverso:

Passo 2

Para o intervalo de confiança, temos que:

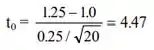
E por fim aplicando MDS de fisher:

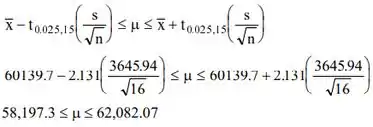
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Seç. 13.5, apresentamos um método pelo qual amostras aleatórias de uma distribuição especificada podem ser geradas. Há vários outros métodos pelos quais isto pode ser feito, alguns dos quais são pr

Uma variável aleatória contínua X é uniformemente distribuída sobre·(-1/2 , 1/2) . Uma amostra de tamanho n é obtida de X e a média amostral X - é calculada. Qual é o desvio padrão deX - ?

Verifique que se X 1 , … , X n forem variáveis aleatórias independentes, cada uma tendo uma distribuição exponencial com parâmetro α i , i =1,2,...,n, e se K = min ⁡ ( X 1 , … , X n ) , então K terá u

Suponha que X tenha uma distribuição geométrica com parâmetro p. Seja X1,...,Xn uma amostra aleatória de X e sejam M = max ⁡ ( X 1 , … , X n ) e K = min ⁡ X 1 , … , X n . Estabeleça a distribuição de