Um artigo da revista Prevention abordou uma pesquisa feita junto a 1257 adultos. O artigo observou que, entre os pesquisados, 27% fumavam e 82% dos fumantes tinham tentado parar de fumar ao menos uma vez. Quantos, dentre os pesquisados, são os fumantes que tentaram deixar de fumar ao menos uma vez? Ao nível de 0,05 de significância, teste a firmação de que menos de 25% dos adultos são fumantes que tentaram deixar o fumo ao menos uma vez.

Agora vamos definir a estatística relevante para esse problema.

Outra parada: vamos ver se podemos aproximar a nossa distribuição pela distribuição normal.

Então a nossa distribuição é aproximada pela distribuição normal.

Como vamos trabalhar com uma distribuição normal, o passo agora é calcular a estatística de teste.

Como o nosso teste é unilateral esquerdo, temos na cauda esquerda, então procuramos uma área de na tabela ai de baixo. O valor mais próximo disso também serve.

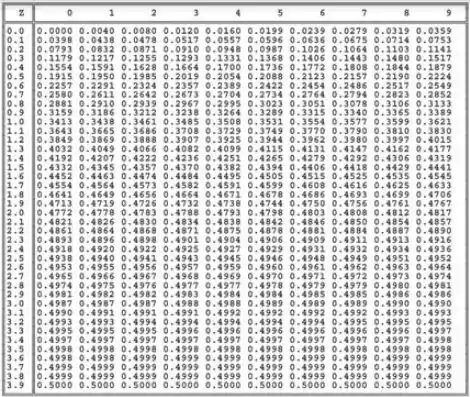
Pela tabela, obtemos o valor crítico:

Vamos dar uma olhada no gráfico abaixo:

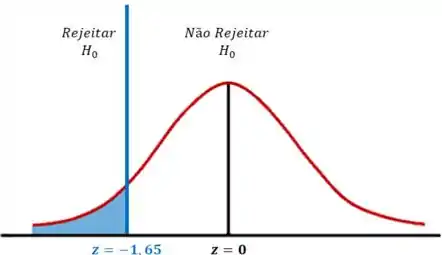
Como está dentro da região crítica, rejeitamos a hipótese nula .

Por fim, vamos calcular o valor P: procurando na tabela do passo 3, vemos que a área correspondente a esse valor é 0,4909, então:

Como o valor P é menor que , rejeitamos .