Uma pesquisa da Bruskin-Goldring Research junto a 1012 adultos mostrou que, entre os que compram tortas de frutas, 28% as comem, e 72% as destinam a outras finalidades, como calços de porta, alimento de pássaros e aterro. Isto surpreendeu os fabricantes de tortas de frutas, que supunham que essas tortas fossem um alimento apreciado. O presidente da Kansas Food Products Company alega que os resultados da pesquisa são falsos e que, na realidade, metade de todos os adultos consomem suas tortas de frutas. Teste essa afirmação, ao nível de 0,01 de significância. Com base no resultado, acha que o fabricante das tortas de frutas deve cogitar de modificações para tornar seu produto mais atraente como alimento, ou mais adequado a outros usos?

Agora vamos definir a estatística relevante para esse problema.

Outra parada: vamos ver se podemos aproximar a nossa distribuição pela distribuição normal.

Então a nossa distribuição é aproximada pela distribuição normal.

Como vamos trabalhar com uma distribuição normal, o passo agora é calcular a estatística de teste.

Como o nosso teste é bilateral, temos em cada cauda, então procuramos uma área de na tabela ai de baixo. O valor mais próximo disso também serve.

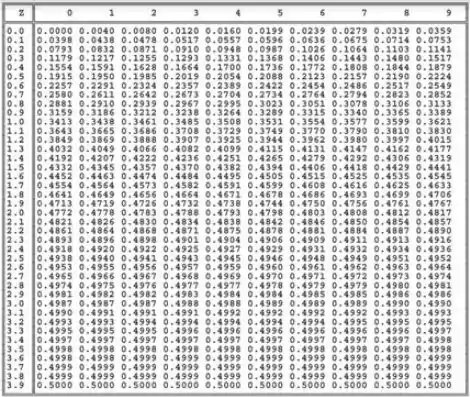
Pela tabela, obtemos o valor crítico:

Vamos dar uma olhada no gráfico abaixo:

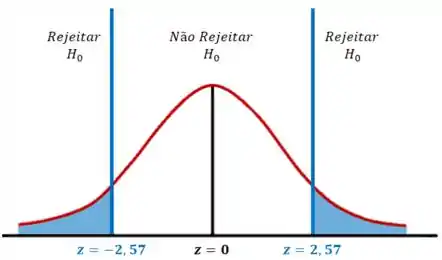
Como está dentro da região crítica, rejeitamos a hipótese nula .

Nesse exercício não conseguimos calcular o valor P, porque não é encontrado na tabela, mas como esse valor de é negativo e bem alto, e o nosso teste é bilateral, podemos supor que o valor P vai ser muito pequeno e menor que , logo, rejeitamos .