Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 14.Exercícios - Ex. 53
Um artigo na revista Textile Research Insitute Journal (1984, Vol. 54, pp.171-179) reportou os resultados de um experimente que estudou os efeitos de tratar tecidos com sais inorgânicos selecionados sobre sobre a inflamabilidade do material. Foram usados dois níveis de aplicação de cada sal e um teste de queima são mostrados a seguir.
Teste as diferenças entre sais, entre níveis de aplicação e entre interações. Use .
Desenhe um gráfico da interação entre o sal e o nível de aplicação. Que conclusões você pode tirar desse gráfico?
Analise os resíduos desse experimento.
Passo 1
Bom galera, considerando a tabela o modelo estatístico linear do experimento é:
As hipóteses que teremos que testar são:
(Não tem efeito no nível)
Pelo menos um
(Não tem efeito no sal)
Pelo menos um
(Não tem interação)
Pelo menos um
Passo 2
Beleza, agora usando o Minitab para fazer a análise de variância. Nós encontraremos:
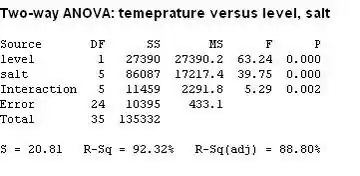
Então, temos que o valor de para o nível de aplicação é menor do que . Portanto, rejeitamos a hipótese nula, logo vemos que o tratamento do tecido é diferente para o nível de aplicação diferente.
Já o valor de para o sal é menor que . Então, podemos rejeitar a hipótese nula e concluímos que os sais inorgânicos afetam o tecido de tratamento.
Por último o valor de para o valor da interação é menor que . Portanto, rejeitamos a hipótese nula e concluímos que há interação entre o nível e o sal.
Passo 3
Show de bola, ainda no Minitab, podemos gerar um gráfico da interação:
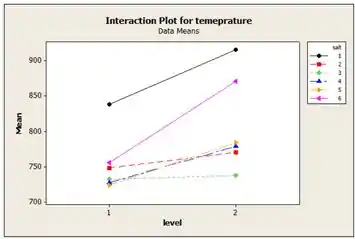
Com esse gráfico, podemos ver que há uma interação entre os níveis de aplicação e os sais, uma vez que todas as seis linhas não são paralelas. A maior valor é quando a eficácia no tratamento do tecido é maior. Portanto, o nível de aplicação com sal não tratado é o mais eficaz.
Passo 4
Por fim, ainda no Minitab, geramos os gráficos dos resíduos:
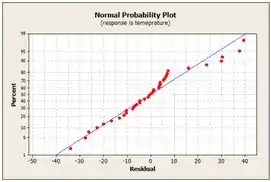
No gráfico, temos a parcela de probabilidade normal de resíduos. Esse gráfico tem pontos que caem um pouquinho fora da linha reta, isso indica que há alguns problemas com a suposição de normalidade.
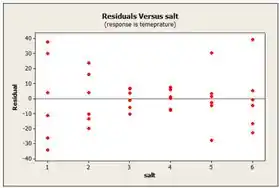
Já no e gráfico representam a parcela de resíduos versus o nível e o sal, respectivamente. Com o gráfico vemos que o nível de aplicação tem maior variabilidade no tratamento do tecido do que o nível de aplicação . O sal não tratado (chamado de ) proporciona mais variabilidade no tratamento do tecido do que outros sais.
E no gráfico de resíduos versus valor ajustado mostra os resíduos mais elevados à medida que o valor da resposta aumenta. Isso sugere que, é preciso haver alguma transformação da variável resposta.
Resposta
O nível de aplicação e os sais inorgânicos afetam o tecido do tratamento e há interação entre o nível de aplicação e os sais inorgânicos.
O nível de aplicação com sal não tratado é o mais eficaz.