Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 13.Exercícios Suplementares - Ex. 71
Um banho de amônia é um dos mais amplamente usados para sedimentar revestimentos de liga . O artigo "Modelling of Palladium and Nickel in an Amonia Bath in a Rotary Device" (Plating and Surface Finishing, 1997, p. 102-104) apresentou um estudo sobre como as características de composiçāo do banho influenciam nas propriedades do revestimento.Considere os dados a seguir sobre concentraçāo de concentraçāo de , temperatura densidade de corrente catódica e conteúdo de paládio (%) do revestimento.
a. Ajuste o modelo de primeira ordem aos cinco previsores e avalie sua utilidade. Todos os previsores parecem importantes?
b. Ajuste o modelo completo de segunda ordem e avalie sua utilidade.
c. O grupo de previsores de segunda ordem (de interação e quadráticos) parecem fornecer informações mais úteis sobre do que os previsores de primeira ordem? Realize um teste apropriado das hipóteses.
d. Os autores do artigo citado sugeriram que fossem usados todos os cinco previsores de primeira ordem mais o previsor extra . Ajuste esse modelo. Todos os seis previsores parecem importantes?
Passo 1
E aí pessoal partiu para mais uma questão de (probabilidade)? Abaixo começaremos trazendo algumas informações do enunciado:
Ajuste o modelo de primeira ordem aos cinco previsores e avalie sua utilidade. Todos os previsores parecem importantes?
a.Usando o Minitab para gerar o modelo de regressão de primeira ordem, testamos a utilidade do modelo (para ver se algum dos preditores é útil) e com f=21,03 e um valor de p de 0,000, determinamos que pelo menos um dos preditores é útil na previsão do conteúdo de paládio. Olhando para os preditores individuais, o valor de p associado ao preditor de pH tem valor 0,169, o que indicaria que este preditor não é importante na presença dos outros.
Passo 2
Ajuste o modelo completo de segunda ordem e avalie sua utilidade.
b. Testando vs. pelo menos um dos . Com estatística calculada f=6,29 e valor p 0,002, esse modelo também é útil em qualquer nível de significância razoável.
Passo 3
O grupo de previsores de segunda ordem (de interação e quadráticos) parecem fornecer informações mais úteis sobre do que os previsores de primeira ordem? Realize um teste apropriado das hipóteses.
c. Testando vs. pelo menos um dos listados, a estatística de teste é. Usando o nível de significância .05, a região de rejeição seria.. Como 1,07
Resposta
Os autores do artigo citado sugeriram que fossem usados todos os cinco previsores de primeira ordem mais o previsor extra . Ajuste esse modelo. Todos os seis previsores parecem importantes?
Segue a saída parcial do Minitab, que mostra todos os preditores como significativos no nível 0,05:
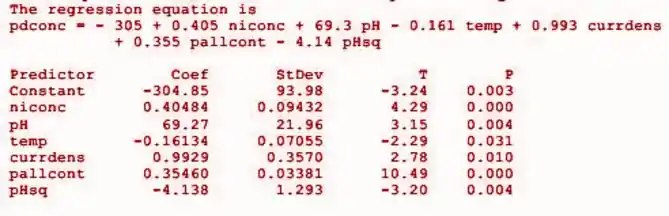
Resposta
a. Olhando para os preditores individuais, o valor de p associado ao preditor de pH tem valor 0,169, o que indicaria que este preditor não é importante na presença dos outros.
b. Com estatística calculada f=6,29 e valor p 0,002, esse modelo também é útil em qualquer nível de significância razoável.
c. Eles não adicionam informações suficientes para tornar este modelo significativamente melhor do que o modelo simples de primeira ordem.
d. mostra todos os preditores como significativos no nível 0,05:
Espero que tenham aprendido com essa questão, até a próxima !