Bay Photo é uma firma de fotografia de São Francisco que deseja fazer uma campanha publicitária por telefone. Um dos sócios argumenta que clientes potenciais que não têm seus números no catálogo telefônico não serão atingidos, mas o gerente de marketing afirma que menos da metade dos residentes de São Francisco não têm seus números no catálogo telefônico. Em uma amostra aleatória de 400 telefones residenciais de S. Francisco, 39% não estavam listados. Utilize um nível de significância de 0,005 para testar a afirmação do gerente de marketing.

Agora vamos definir a estatística relevante para esse problema.

Outra parada: vamos ver se podemos aproximar a nossa distribuição pela distribuição normal.

Então a nossa distribuição é aproximada pela distribuição normal.

Como vamos trabalhar com uma distribuição normal, o passo agora é calcular a estatística de teste.

Como o nosso teste é unilateral esquerdo, temos na cauda esquerda, então procuramos uma área de na tabela ai de baixo. O valor mais próximo disso também serve.

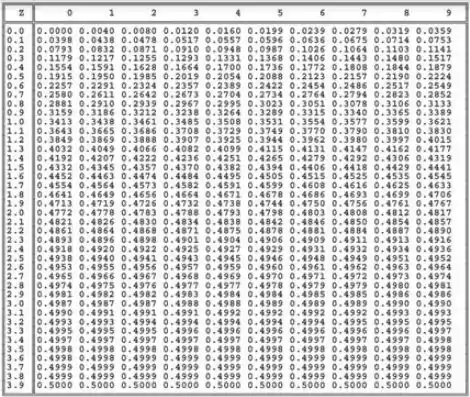
Pela tabela, obtemos o valor crítico:

Vamos dar uma olhada no gráfico abaixo:

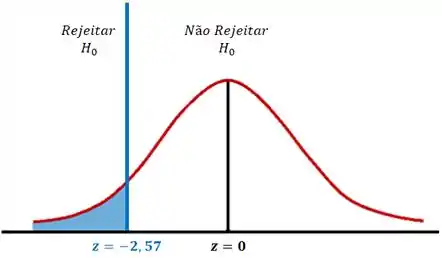
Como está dentro da região crítica, rejeitamos a hipótese nula .

Nesse exercício não conseguimos calcular o valor P, porque não é encontrado na tabela, mas como esse valor de é negativo e alto, e o nosso teste é unilateral esquerdo, podemos supor que o valor P vai ser muito pequeno e menor que , logo, rejeitamos .