Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 8.Exercícios propostos - Ex. 17b

Certas válvulas produzidas por uma empresa têm vida média de 900 h e desvio padrão de 80 h. A empresa envia 1.000 lotes, de 100 válvulas cada um. Em quantos lotes pode-se esperar que:

  1. os desvios padrões da vida média excedam a 95 h?

Passo 1

Olá galera, vem comigo! Pelo enunciado temos os seguintes dados:

  • μ = 900 ;
  • σ = 80 ;
  • n = 100 .

Para este exercício queremos saber a quantidade de lote para que os desvios padrões da vida média excedam a 95 h. Então temos:

S = 95

Como queremos saber em relação ao desvio padrão, iremos primeiramente utilizar o Teorema de Fisher, para definirmos o valor de alfa através da tabela da Distribuição qui-quadrado:

X n - 1 2 = S 2 σ 2 ∙ n - 1 = 95 2 80 2 ∙ 100 - 1 = 139,6

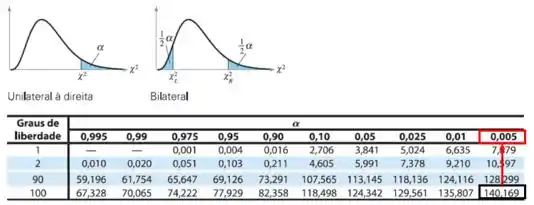
Assumindo que:

α 2 = 0,005 → α = 0,01

Passo 2

Para descobrirmos o valor z , iremos utilizar a distribuição de t de Student. Com:

  • α = 0,01 ;
  • ϕ = n - 1 = 99 .

Pela tabela da distribuição t :

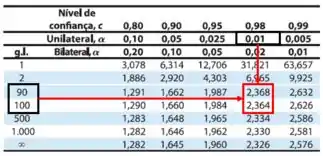
Fazendo uma interpolação, para descobrirmos para ϕ = 99 :

t - 2,364 2,368 - 2,364 = 99 - 90 100 - 90 → t = 2,3676

Passo 3

Pela equação de t de Student

z = 2,3676 ∙ 95 80 = 2,81

Pela tabela da distribuição normal, temos:

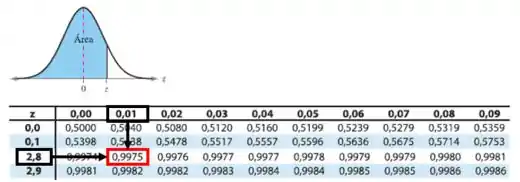
Pela tabela encontramos o valor de P S < 95 , então iremos subtrair de 1:

P S > 95 = 1 - P X < 95 = 1 - 0,9975 = 0,0025

Para 1000 lotes:

0,0025 ∙ 1000 = 2   l o t e s

Tchau galerinha! Te espero em mais exercícios.

Resposta

2   l o t e s .

Exercícios de Livros Relacionados

A probabilidade de um funcionário chegar atrasado pela manhã ao emprego é de 10% . Qual a probabilidade de num certo ano ( 300d i a sd et r a b a l h o ) ele chegar atrasado em menos que 20d i a s ?
Jogando-se um dado 450v e z e s , qual a probabilidade de se obter face maior que 4 em mais que 30% das jogadas?
Um dado é jogado 600 vezes. Determinar a probabilidade de que o número de vezes em que sai face 1 , difira da média por mais que 30v e z e s .
O IBC determinou, a partir de várias experiências, que 5% das sementes de café não germinavam. Estas sementes são vendidas em pacotes de 400 unidades, com a garantia de que pelo menos 92% delas germin
Sabe-se que 20% das peças produzidas por umas siderúrgicas são defeituosas. Selecionando-se, ao acaso e com reposição, 100 peças da produção, qual a probabilidade de encontrarmos de 15 a 30 defeituosa