Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 8.Exercícios propostos - Ex. 6a
Certos amortecedores fabricados por uma empresa têm uma vida média de 800 dias e desvio padrão de 60 dias. Determinar a probabilidade de uma amostra aleatória de 16 amortecedores, retirados do grupo, ter a vida média:
- entre 770 e 830 dias.
Passo 1
Oi pessoal. Vamos pensar juntos neste exercício?! Iremos iniciar relembrando de algumas teorias.
Ao retirar uma amostra aleatória de uma população, cada valor da amostra constitui uma variável aleatória cuja distribuição de probabilidades é a mesma da população no instante da retirada desse elemento para a amostra.
Se é uma população de média e variância , na qual se extrai uma amostra aleatória de elementos (, , , ). Sabe-se que , representa a média amostral:
Uma variável aleatória, obtida pela combinação linear de variáveis aleatórias normais independentes, tem também distribuição normal. Se a distribuição da população for normal, a distribuição amostral de também será normal, para qualquer tamanho de amostra. A figura a seguir representa um caso genérico, envolvendo a distribuição amostral de , no caso de população normal.
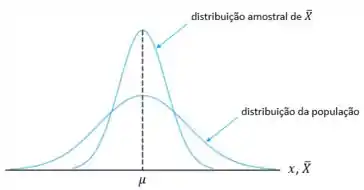
Podemos observar que quanto maior o tamanho da amostra, menor será a variância de .
Passo 2
A variável normal padronizada da variável :
Pelo enunciado temos os seguintes dados:
- ;
- ;
- .
E queremos saber a probabilidade de ter a vida média entre 770 e 830 dias, ou seja:
Passo 3
Então para :
Pela Tabela da Distribuição normal, temos:
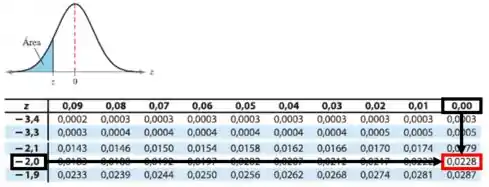
E para :
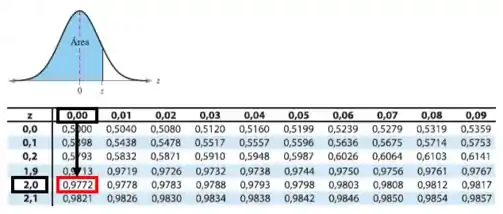
Então a probabilidade de uma amostra aleatória de 16 amortecedores ter a vida média entre 770 e 830 dias é:
Tchau galerinha! Te espero em mais exercícios.
Resposta
.