Enunciado
Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 2.4 - Ex. 48
Comparando dois conjuntos de dados. Encontre o coeficiente de variação para cada um dos conjuntos de dados. Então, compare os resultados.
Idade e pesos. As idades (em anos) e os pesos (em libras) de todos os rebatedores do San Diego Chargers em 2012 estão listados a seguir. (Fonte: ESPN.)
Passo 1
Vamos resolver esse exercício juntos? Então, vamos lá!
Para o cálculo do coeficiente de variação (CV), usamos a seguinte equação:
Antes disso, precisamos encontrar a média e o desvio padrão populacional:
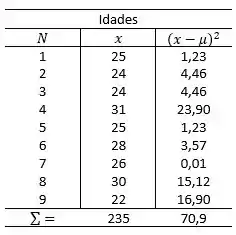
Média populacional das Idades:
Desvio padrão populacional das Idades:
Coeficiente de variação para Idades:
Passo 2
Agora iremos calcular o CV para os Pesos:
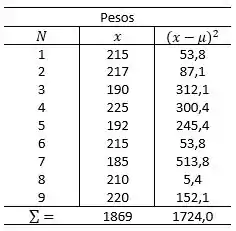
Média populacional dos Pesos:
Desvio padrão populacional dos Pesos:
Coeficiente de variação para os Pesos:
Resposta
As idades (10,7%) são mais variáveis que os pesos (6,6%) para todos os rebatedores do San Diego Chargers em 2012.