O conjunto de dados a seguir está relacionado àquele do Exercício 1.24. Eles dão a porcentagem de famílias que estão no mais alto nível de renda nas mesmas escolas, na mesma ordem do exercício anterior.
72,2 31,9 26,5 29,1 27,3 8,6 22,3 26,5 20,4 12,8 25,1 19,2 24,1 58,2 68,1 89,2 55.1 9,4 14,5 13,9 20,7 17,9 8,5 55,4 38,1 54,2 21,5 26,2 59,1 43,3
(a) Calcule a média amostral.
(b) Calcule a mediana amostral.
(c) Construa um histograma de freqüências relativas dos dados.
(d) Calcule a média aparada a 10%. Compare com os resultados de (a) e (b) e comente.
Passo 1
Os dados que são informados no enunciado são em referência renda das famílias dos alunos do exercício anterior, sendo a porcentagem de famílias que estão com um alto nível de renda, com escolas.
Passo 2
Para definirmos a média amostral temos a seguinte equação:
Então, temos o somatório de todos os dados da tabela dividido pelo número de escolas.
Passo 3
Para realizarmos o cálculo da mediana, como temos um número par de escolas, precisamos encontrar as duas porcentagens que estão entre as menores e maiores. Sendo, neste exemplo, e . Pela organização abaixo é possível visualizar melhor:
Portanto, a mediana é dada por:
Passo 4
Primeiro, vamos montar a distribuição de frequência relativa. Onde, o ponto médio é o meio do intervalo observado.
A distribuição pode ser analisada a seguir:
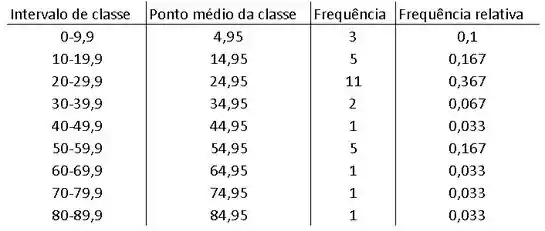
O histograma pode ser analisado abaixo:
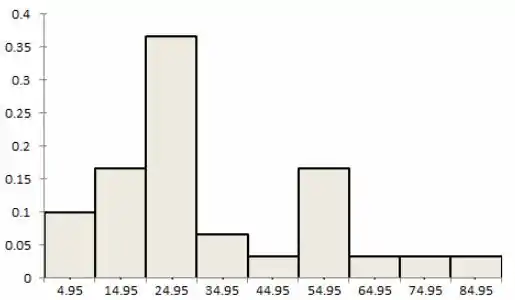
Passo 5
Para encontrarmos a média aparada em das 30 amostras, significa que precisamos remover as 3 menores e as 3 maiores porcentagens, ficando os novos dados:
Calculando a média:
Podemos notar, que é maior do que e , o que significa que temos valores extremos.
Resposta
(a) .
(b) .
(c) Passo 4.
(d) .