Os conjuntos de dados a seguir consistem de 25 observações sobre resistência a fratura do prato de base do aço temperado com níquel a (de "Fracture Testing of Weldments", ASTM Special Publ. No. 381, 1965, p. 328-356). Utilize o gráfico de probabilidade normal do teste de coeficiente de correlação para decidir se uma distribuição normal fornece um modelo plausível para resistência à fratura.
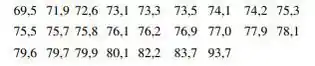
Passo 1
E aí pessoal partiu para mais uma questão de (probabilidade)? Abaixo começaremos trazendo algumas informações do enunciado:
Vamos pegar os valores do enunciado e tabular os erros com a ajuda do minitab.

OBS: Minitab foi usado para calcular 's. ,
mesmo no nível de significância muito menor de 0,01, a hipótese nula de normalidade da população deve ser rejeitada (a maior observação parece ser a principal culpada).
Resposta
mesmo no nível de significância muito menor de 0,01, a hipótese nula de normalidade da população deve ser rejeitada (a maior observação parece ser a principal culpada).
Espero que tenham aprendido com essa questão, até a próxima !