Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 7.Exercícios - Ex. 32
Considere a função densidade de probabilidade
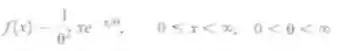
Encontre o estimador de máxima verossimilhança para theta.
Passo 1
A função de densidade de probabilidade é:
Vamos encontrar o estimador de máxima verossimilhança para .
Passo 2
Aplicando log nos dois lados…
Diferenciando em relação à e igualando à zero, nós chegamos em:
Resposta
Exercícios de Livros Relacionados
(c) O diretor de vendas anunciou que transferirá para outra praça todos os vendedores cujo volume de vendas for inferior ao 1° quartil da distribuição. Qual o volume mínimo de vendas que um vendedor d
(g) Qual o grau de associação entre o conceito do gerente e o resultado do teste? E entre zona e vendas?
Use o problema anterior para construir histogramas para:Variável umid (umidade) do CD-Poluição;
Use o problema anterior para construir histogramas para:(c) a temperatura de Cananéia, do CD-Temperaturas.
Use o problema anterior para construir histogramas para:(b) variável salário dos professores do CD-Salários;