Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 11.Exercícios - Ex. 36
Considere o modelo sem interseção , com os sendo . A estimativa de é e .
a)Planeje uma estatística de teste para contra .
b)Aplique o teste no item (a) para o modelo do Exercício 11-20.
Passo 1
Eae gente, tudo certo com vocês? Espero que sim! Se liga nessa questão: primeiro, temos que para a estatística teste,
O teste no item a, para o modelo da questão 11-20, temos que:
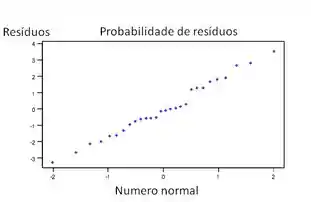
Passo 2
c)O modelo parece adequado. Alguma sugestão de uma variação não constante, pode ser isso:
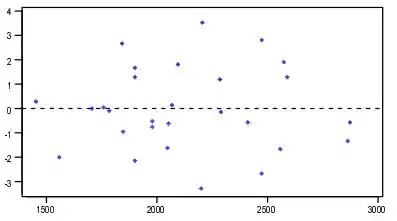
d) Sim, observações 1,8 e 21.
Resposta
O modelo de regressão linear simples tem o menor intervalo. Sim, o modelo simples nesse caso é preferível.
Exercícios de Livros Relacionados
Considere os dados de LNF do exercício 12-15.a)Calcule intervalos de confiança de 95% para cada coeficiente de regressão.b)Calcule um intervalo de confiança de 95% para a faixa útil média quando x1=80
Considere o ajusto do modelo de regressão aos dados da mistura de carvão e calcário do Exercício 12-12. Use densidade como a resposta.a)Calcule intervalos de confiança de 90% para cada coeficiente de
Considere os dados sobre resistência à tração de um fio de exercício 12-6.a)Calcule intervalos de confiança de 99% para cada coeficiente de regressão.b)Calcule um intervalo de confiança de 95% para re
Considere o ajusto do modelo de regressão aos dados da mistura de carvão e calcário do Exercício 12-11. Use densidade como a resposta.a)Calcule intervalos de confiança de 90% para cada coeficiente de
Quando ajustando modelos de regressão polinomial, frequentemente subtraímos x de cada valor x para produzir um regressor “centralizado” x’=x-x. Isso reduz o efeito das dependências entre os termos do