Quando ajustando modelos de regressão polinomial, frequentemente subtraímos x de cada valor x para produzir um regressor “centralizado” x’=x-x. Isso reduz o efeito das dependências entre os termos do modelo e frequentemente conduz as estimativas mais exatas dos coeficientes de regressão. Usando os dados do exercício 12-66, ajuste o modelo .
a)Use os resultados para estimar os coeficientes no modelo n’ao centralizado . Preveja y quando . Suponha que usemos a variável padronizada , em que seja desvio-padrão de x na construção de um modelo de regressão polinomial. Ajusste o modelo .
b)Qual é o valor de y previsto quando x=285F
c)Estime os coeficientes de regressão no modelo não padronizado .
d)O que você pode dizer acerca da relação entre SQe e R2 para os modelos padronizado e não padronizado?
e)Suponha que a variável , seja usada no modelo, juntamente com x. Ajuste o modelo e comente a relação entre SQ e R nos modelos padronizados e não padronizados.
Passo 1
Hey, jovem, tudo bem contigo? Espero que sim 😊 Bora pra mais uma questãozinha de estatística? Vamo que vamo! Então, nessa questão a gente tem que:
a)Para o item:
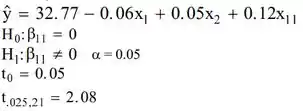
Passo 2
b)Não, os comprimentos desses intervalos não fornecem qualquer informação sobre a contribuição para o modelo do termo de interação.
c)No item temos:
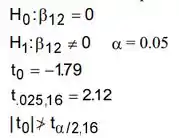
Resposta
Ei, a resposta está no passo a passo :)