Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 10.Problemas - Ex. 36
Considere a população . Retire amostras de tamanho , sem reposição e construa a distribuição amostral de . Obtenha e e verifique (10.9).
Passo 1
Fala ae, pessoal! Bora fazer esse exercício!
Primeiro, vamos construir a distribuição das probabilidades das possíveis amostras de tamanho 2 que podem ser selecionadas sem reposição da nossa população:
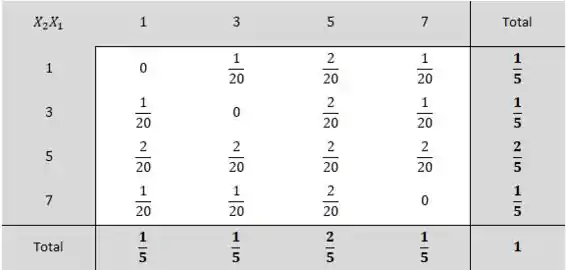
Com essa distribuição, podemos construir a distribuição amostral de :
Passo 2
Sabendo a distribuição amostral de , podemos calcular e :
Passo 3
Por fim, vamos verificar a equação (10.9), que está na seção seguinte do livro. Para isso, vamos calcular a variância da população (), onde :
Verificando a equação (10.9):
Que coincide com o valor calculado utilizando as amostras.
Resposta
Verificando (10.9), vemos que coincide com o valor da variância calculado a partir das amostras.