Para decidirmos se os habitantes de uma ilha são descendentes da civilização A ou B,

iremos proceder do seguinte modo:

(i) selecionamos uma amostra de 100 moradores adultos da ilha, e determinamos a altura

média deles;

(ii) se essa altura média for superior a 176, diremos que são descendentes de B; caso

contrário, são descendentes de A.

Os parâmetros das alturas das duas civilizações são:

Definamos:

— dizer que os habitantes da ilha são descendentes de B quan-

do, na realidade, são de A.

— dizer que são de A quando, na realidade, são de B.

(b) Qual deve ser a regra de decisão se quisermos fixar a probabilidade do em

5%? Qual a probabilidade do , nesse caso?

(c) Se , como ficariam as respostas de (b)?

(d) Quais as probabilidades do , nas condições da questão (b), se a média

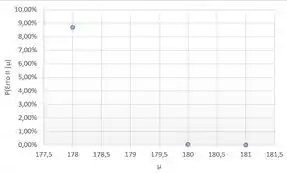
Coloque num gráfico os pares

(C) Para

Logo,

(D) da questão (b): e

1. Para
2. Para
3. Para