Enunciado
Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 1.Exercícios - Ex. 29
Considere a situação do Exercício 1.28, mas agora use o seguinte conjunto de dados, no qual o encolhimento é medido novamente em velocidades de injeção baixa e alta. Entretanto, dessa vez a temperatura do molde foi elevada para um nível ‘alto’ e mantida constante. Valores de encolhimento em velocidade de injeção baixa:
Os valores de encolhimento em velocidade de injeção alta são:
(a) Como no Exercício 1.28, construa um diagrama de pontos de ambos os conjuntos de dados e identifique ambas as médias (ou seja, a média de encolhimento para velocidade de injeção baixa e alta).
(b) Como no Exercício 1.28, comente a influência da velocidade de injeção no encolhimento para temperatura alta do molde. Leve em consideração a posição das duas médias e a variabilidade em torno de cada uma.
(c) Compare suas conclusões em (b) com aquelas em (b) do Exercício 1.28, no qual a temperatura do molde foi mantida no nível baixo. Você diria que há uma interação entre a velocidade de injeção e a temperatura do molde? Explique.
Passo 1
Falaa, meu querido/minha querida. Para resolvermos essa questão, precisamos primeiro calcular as médias amostral para os encolhimentos em injeção em baixa e alta velocidade, e depois plotarmos os gráficos. Por fim, basta fazermos algumas explicações na letra (b) e (c). Bora lá!!!
Passo 2
Para calcularmos a média amostral usamos a seguinte fórmula:
Então, para o encolhimento em injeção de baixa velocidade:
Para o encolhimento em injeção de alta velocidade:
Plotando os gráficos, para o encolhimento em injeção de baixa velocidade:
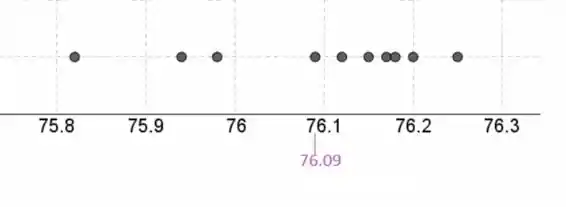
Para o encolhimento em injeção de alta velocidade:
Em roxo foram destacados os pontos onde se encontram as médias amostrais.
Passo 3
Uma injeção de velocidade mais alta aumenta a contração, pois, podemos notar que todos os pontos da velocidade de injeção alta são maiores do que os pontos da injeção de baixa velocidade.
Passo 4
Por fim, podemos concluir que existe uma interação entre a velocidade de injeção e a temperatura do molde. Pois, podemos notar uma mudança do exemplo anterior em diferentes temperaturas.
Resposta
Resolução nos passos anteriores.