Determinou-se o custo de operação por cliente para cada uma de 12 organizações. Os 12 valores têm média de $2133 e desvio padrão de $345 (com base em dados de “Organizational Comunnication and Performance”, por Snyder e Morris, Journal of Applied Psychology, Vol. 69, No. 3). Ao nível de 0,01 de significância, teste a afirmação de um acionista, que se queixa de que a média para todas as organizações desse tipo excede $1800 por cliente.

Devemos verificar qual tipo de teste vai ser utilizado. Como a nossa amostra ( é menor que 30, podemos utilizar a distribuição de Student:

Vamos calcular o nosso valor crítico....

É só calcular o grau de liberdade :

Agora pela tabela A-3, cruzando os valores de e GL, nós encontramos nosso valor .

Com base na nossa hipótese alternativa , observamos se o teste lateral vai ser direito ou esquerdo.

Vamos ter um teste lateral direito!

Nosso gráfico de distribuição vai ficar assim:

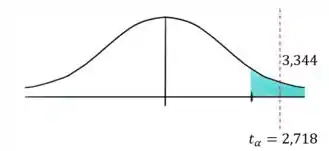
Como o nosso valor está dentro dos limites críticos do gráfico, podemos rejeitar a hipótese nula .

Resposta

Podemos rejeitar a hipótese nula . Assim, o acionista da empresa pode afirmar que a média para todas as organizações desse tipo excede $1800 por cliente.

Próxima questão....