Enunciado
Probabilidade e Estatística - Triola - Introdução à Estatística- Ed: 7º - Capítulo 7.4 - Ex. 16
Um teste de leitura feito com 15 estudantes de terceiro grau acusou e . (“Os dados se baseiam em “A Longitudinal Study of the Effects of Retention/Promotion on Academic Achievement”, por Peterson et al., American Educational Research Journal, Vol. 24 Nº 1.) Esta media amostral de terceiro grau difere significativamente de uma média de 41,9 de uma população de primeiro grau? Tome .
Passo 1
Fala galera! Vamos resolver mais uma questão!
O primeiro passo pra responder essa questão é selecionar os dados.
Como a nossa hipótese alternativa possui uma igualdade, teremos um teste bilateral.
Passo 2
Devemos verificar qual tipo de teste vai ser utilizado. Como a nossa amostra ( é menor que 30, podemos utilizar a distribuição de Student:
Passo 3
Vamos calcular o nosso valor crítico....
É só calcular o grau de liberdade :
Agora pela tabela A-3, cruzando os valores de e GL, nós encontramos nosso valor .
Nosso gráfico de distribuição vai ficar assim:
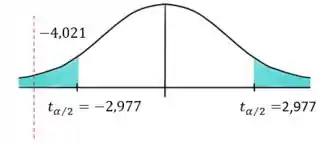
Como o nosso valor está dentro dos limites críticos do gráfico, então podemos rejeitar a hipótese nula .
Resposta
Rejeitamos a hipótese nula .Portanto, a media amostral de terceiro grau difere significativamente de uma média de 41,9 de uma população de primeiro grau.
Era só isso... Vamos resolver outra?
Resposta
Ei, a resposta está no passo a passo :)