Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 6.3 - Ex. 28a

Na distribuição X tilde N (mu ; sigma^2) , encontre:

  1. P (X >= mu + 2 sigma)

Passo 1

Lembrando que quando temos uma variável com distribuição normal, precisamos utilizar uma aproximação para a forma padrão dessa variável; é assim:

Z = (X - mu)/(sigma) tilde N ( 0,1 )

Quando tivermos uma probabilidade, teremos o seguinte:

P (b <= X <= c) = P ((b - mu)/(sigma) <= Z <= (c - mu)/(sigma))

Passo 2

Para a alternativa A, vamos ter:

P (X >= mu + 2 sigma) = P (Z >= ((mu + 2 sigma) - mu)/(sigma)) = P ( Z >= 2 )

Ou seja, basta que procuremos na tabela de distribuição normal, o valor de:

P ( Z >= 2 ) = P (Z >= 0) - P ( 0 <= Z <= 2 )

Lembrando sempre que o gráfico é simétrico e portanto cada metade vale 0,5; em outras palavras:

P (Z <= 0) = P (Z >= 0) = 0,5

Passo 3

Buscando na tabela o valor de P ( 0 <= Z <= 2 ) :

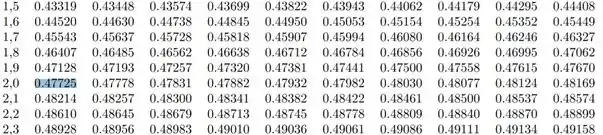
Ou seja,

P (0 <= Z <= 2) = 0,47725

Portanto:

P (Z >= 2) = 0,5 - 0,47725 = 0,02275

Resposta

  1. P (X >= mu + 2 sigma) = 0,02275
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que ambas as curvas de regressão da média sejam, de fato, lineares. Particularmente, admita que E Y x =- 3 2 x - 2 e E X y =- 3 5 y - 3 . Determine o coeficiente de correlação e as esperanças.
Considere a previsão de tempo com duas possibilidades: “chove” ou “não chove” nas próximas 24 horas. Suponha que p = P r o b c h o v en a sp r ó x i m a s24h o r a s1 2 ó . O previsor marca 1 ponto se
Demonstre o teorema 7.17.
Demonstre o teorema 7.16.
Para a variável aleatória (X,Y) definida no Probl. 6.14, calcule E X y , E Y x e verifique que E X = E E X Y e E Y = E E Y X .