Elvis ainda está vivo? O USA Today publicou uma reportagem sobre uma pesquisa da Universidade da Carolina do Norte feita junto a 1248 adultos do sul dos EUA. Constatou-se que 8% dos pesquisados creem que Elvis Presley ainda está vivo. O artigo começa com a afirmação de que “quase 1 em cada 10” sulistas ainda acredita que Elvis esteja vivo. Ao nível de 0,01 de significância, teste a afirmação de que a verdadeira percentagem é inferior a 10%. Com base no resultado, determine se o resultado amostral de 8% justifica a expressão “quase 1 em cada 10”.
Passo 1
Fala ae, pessoal! Bora fazer esse exercício de teste de hipóteses!
Seguindo o procedimento padrão para o teste de hipóteses, primeiro vamos dizer qual é a nossa hipótese nula e a nossa hipótese alternativa nesse problema:
Onde é a nossa hipótese original.
Passo 2
Agora vamos definir a estatística relevante para esse problema.
Outra parada: vamos ver se podemos aproximar a nossa distribuição pela distribuição normal.
Então a nossa distribuição é aproximada pela distribuição normal.
Passo 3
Como vamos trabalhar com uma distribuição normal, o passo agora é calcular a estatística de teste.
Como o nosso teste é unilateral esquerdo, temos na cauda esquerda, então procuramos uma área de na tabela ai de baixo. O valor mais próximo disso também serve.
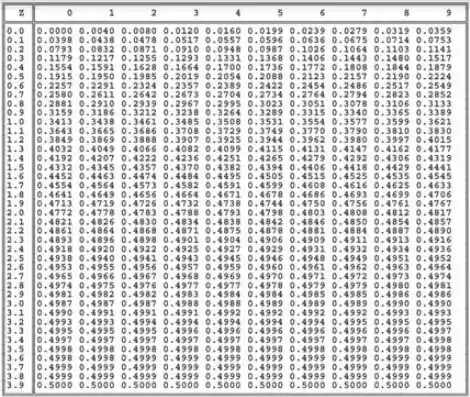
Pela tabela, obtemos o valor crítico:
Passo 4
Vamos dar uma olhada no gráfico abaixo:
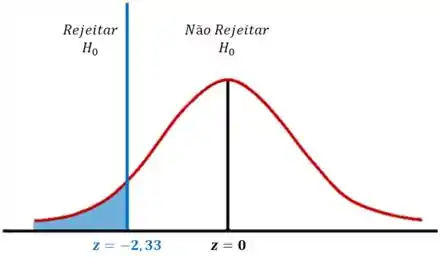
Como está dentro da região crítica, rejeitamos a hipótese nula .
Resposta
Os dados amostrais apoiam a afirmação de que a verdadeira percentagem dos pesquisados creem que Elvis Presley ainda está vivo é inferior a 10%. Com base no resultado obtido, vemos que o resultado é consistente com a expressão “quase 1 em cada 10”.