Enunciado
Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 4.1 - Ex. 37
Encontrando o valor esperado Nos exercícios 37 e 38, encontre o ganho líquido esperado do jogador para uma rodada do jogo. Se x é o ganho líquido de um jogador em um jogo de azar, então E(x) é usualmente negativo. Esse valor dá a quantidade média por jogo que o jogador pode esperar perder.
37. Em um jogo de roleta, a roda tem 38 números, 00, 0, 1, 2, ..., 34, 35 e 36, marcados em posições igualmente espaçadas. Se um jogador aposta $ 1 em um número e ganha, então ele continua com o valor e recebe $ 35 adicionais. Caso contrário, o valor inicial ($ 1) é perdido.
Passo 1
Fala galerinha boa, tudo bem? Vamos para mais uma questão de distribuição de probabilidades. Para calcular o valor esperado em probabilidades temos a seguinte fórmula:
Onde x será o valor dado na distribuição e o valor de cada probabilidade associada a x.
Passo 2
O problema nos diz que o jogador ganha $35 se acertar o número, porém, perde $1 a cada jogada se não cair no número apostado.
Deste modo, temos que construir a tabela da distribuição de probabilidades, o que facilita muito nosso entendimento e resolução do exercício.
São 38 números dentro da aposta. Sendo assim, a cada 1 chance em 38 ele ganha $35 e a cada 37 chances em 38 ele perde $1.
Sendo X a variável aleatória que corresponde ao ganho ou perda do nosso jogador nessa aposta, temos que:
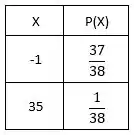
A tabela também pode ser escrita da seguinte forma:
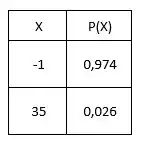
Passo 3
O próximo passo é calcular o valor esperado desse ganho, baseado nas probabilidades da tabela anterior:
Nesse caso, nosso jogador vai perder em média, aproximadamente, $0,05 por jogada. Não é à toa que chamamos de “jogo de azar”.
E é isso galerinha. Até a próxima!