Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 12.Problemas - Ex. 23
Estamos desconfiados de que a média das receitas municipais per capita das cidades pequenas
é maior do que a das receitas do estado, que é de 1.229 unidades.
Para comprovar ou não essa hipótese, sorteamos dez cidades pequenas, e obtivemos os
seguintes resultados:
1.230; 582; 576; 2.093; 2.621; 1.045; 1.439; 717; 1.838; 1.359.
Obs.: Para facilitar os cálculos, informamos que a soma das observações é 13.500, e a
soma dos quadrados das observações é 22.335.650 (13.5002 = 182.250.000).
(a) Mostre que o teste de hipótese usado, com, levará à aceitação de que a
média das cidades pequenas é igual à do estado.
(b) Você não acha estranha essa conclusão quando observa que a média da amostra
obtida é bem maior do que a média do estado? Como você explicaria isso?
Passo 1
Vamos definir nossa variável:
Do ununciado:
Considerando que a população tenha distribuição normal.
Passo 2
- Para realizar o teste de hipótese para a média, devemos considerar que a variância populacional é desconhecida, usamo a seguinte aproximação;
Teste de hipótese:
Vamos construir nossa Região crítica:
Onde:
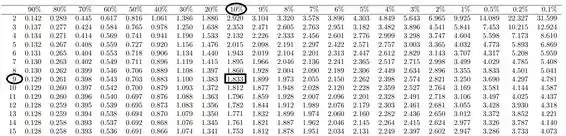
Lembrando que na distribuição de t-student, quando temos uma Rc unilateral,
Portanto nossa região critica fica assim:
Passo 3
Teste sob
Como não pertence à região critica, não rejeitamos , e portanto existem evidencias de que a receita média per capita das cidades é igual à receita média do estado.
Resposta
- Não rejeitamos , há evidencias de que a receita média das cidades pequenas seja igual à receita do estado.
- Apesar da receita média obtida dos municípios ser maior do que a do estado, ela apresenta uma alta variância, que evidencia a dispersão dos valores obtidos.