Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 12.Problemas - Ex. 5

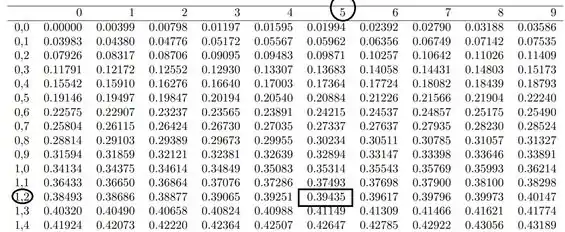
A variável X , custo de manutenção de um tear, pode ser considerada como tendo distribui-

ção normal de m é d i a   μ e desvio padrão de 20 unidades. Os valores possíveis de μ podem ser

200 ou 210. Para verificar qual dos dois valores é o mais provável, usar-se-á uma amostra

de 25 teares. Defina:

(a) Uma hipótese a ser testada.

(b) Uma regra de decisão e encontre as probabilidades dos erros de tipo I e II.

Passo 1

Do enunciado:

X ~ N μ ; 20 2

Podemos usar a seguinte aproximação:

Z = X - - μ σ 2 n ~ N ( 0,1 )

Então, podemos construir o seguinte teste de hipótese:

  1. H 0 : μ = 200       e       H 1 :   μ = 21 0

    Passo 2

  2. Vamos adotar a seguinte Região Crítica:

R C = { X - ≥ 205 }

α = P E r r o   I = P r e j e i t a r   H 0 H 0 é   v e r d a d e i r a = P X - ≥ 205 X - ~ N ( 200   ; 20 2 ) ) =

P X - - μ σ 2 n ≥ 205 - μ σ 2 n = P Z ≥ 205 - 200 20 2 25 = P Z ≥ 1,25 = 0,5 - 0,39435 = 0 , 10565 ‬

Passo 2

E

β = P E r r o   I I = P a c e i t a r   H 0 H 0   é   f a l s o = P X - < 205 X ~   N ( 210 ; 20 2 ) ) =

P Z < 205 - 210 20 2 25 = P Z < - 1,25 = 0,5 - 0,39435 = 0,10565

Resposta

  1. H 0 : μ = 200       e       H 1 :   μ = 21 0
  2. R C = X - ≥ 205   e   α = β = 10,5 %
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para decidirmos se os habitantes de uma ilha são descendentes da civilização A ou B,iremos proceder do seguinte modo:(i) selecionamos uma amostra de 100 moradores adultos da ilha, e determinamos a alt
Para decidirmos se os habitantes de uma ilha são descendentes da civilização A ou B,iremos proceder do seguinte modo:(i) selecionamos uma amostra de 100 moradores adultos da ilha, e determinamos a alt
Da população X~ N ( 50 ,100 ) retirou-se uma amostra casual simples de tamanho n=10 , calculando-se o valor de X - ,Seor e s p e c t i v ov a l o rd et .SeP ( X–50t S 10 )=90 % , encontre o valor de t
Estamos desconfiados de que a média das receitas municipais per capita das cidades pequenas ( 0–20.000h a b i t a n t e s ) é maior do que a das receitas do estado, que é de 1.229 unidades.Para compro
Deseja-se estimar qual a porcentagem média da receita familiar gasta com alimentaçãopelos moradores de uma grande vila industrial. Para isso, selecionou-se uma amostra de16 famílias, que apresentou os